题目内容
(本小题满分14分)已知动圆过定点F(2,0),且与直线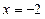 相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线
相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线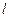 与轨迹C交于A、B两点,且这两点的横坐标分别为
与轨迹C交于A、B两点,且这两点的横坐标分别为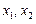 .①求证:
.①求证: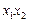 为定值;②试用
为定值;②试用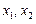 表示线段AB的长度;③求线段AB长度的最小值。
表示线段AB的长度;③求线段AB长度的最小值。
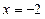 相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线
相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线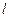 与轨迹C交于A、B两点,且这两点的横坐标分别为
与轨迹C交于A、B两点,且这两点的横坐标分别为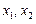 .①求证:
.①求证: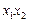 为定值;②试用
为定值;②试用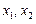 表示线段AB的长度;③求线段AB长度的最小值。
表示线段AB的长度;③求线段AB长度的最小值。(Ⅰ)
 (Ⅱ) 见解析
(Ⅱ) 见解析(1)设动圆圆心
 ,则
,则 ,化简得
,化简得
(2)设直线
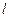 :
:
①由
 得
得 ,且
,且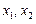 就是方程的两个根,
就是方程的两个根,所以
 为定值。
为定值。 ②根据题意知,这是过焦点的弦,由抛物线的定义得
 ;
;③
 且
且 ,所以
,所以 ,当且仅当
,当且仅当 时取“=”,所以线段AB的长度的最小值为
时取“=”,所以线段AB的长度的最小值为

练习册系列答案
相关题目
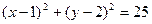 ,直线
,直线 :
: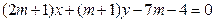
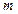 为何值时,直线
为何值时,直线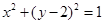 相切,且在每坐标轴上截距相等的距离有( )
相切,且在每坐标轴上截距相等的距离有( )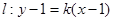 和圆
和圆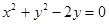 的位置关系是 ( )
的位置关系是 ( )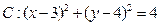 ,直线
,直线 过定点A(1,0).
过定点A(1,0).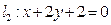 的交点为N,判断
的交点为N,判断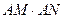 是否为定值,若是,则求出定值;若不是,请说明理由.
是否为定值,若是,则求出定值;若不是,请说明理由.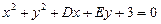 ,圆C关于直线
,圆C关于直线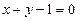 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为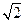
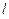 与圆C相切,且在x轴、y轴上的截距相等,求直线
与圆C相切,且在x轴、y轴上的截距相等,求直线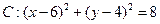 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.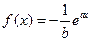 在x=0处的切线
在x=0处的切线 与圆
与圆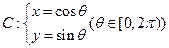 相离,则
相离,则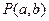 与圆
与圆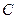 的位置关系是:
的位置关系是: