题目内容

如图1,已知设矩形ABCD(AB＞AD)周长为24,把它关于AC折起来,AB折过去后,交CD于点P,设AB=x,求△ADP的最大面积及相应x值.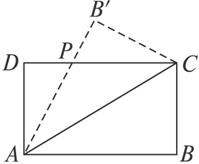

图1

解：∵AB=x,∴AD=12-x.

又∵DP=PB′,

∴AP=AB′-PB′=AB-DP=x-DP.

由勾股定理,得(12-x)2+DP2=(x-DP)2,

即DP=.

∴S△ADP=AD·DP=(12-x)()=108-(6x+).

∵x＞0,∴6x+≥26x·=.

∴S=108-(6x+)≤108-,

当且仅当6x=,即当x=时,S有最大值108-.

答:当x=时,△ADP的面积有最大值108-.

练习册系列答案
相关题目
将一块圆心角为
π
3
半径为a的扇形铁片截成一块矩形，如图，有两种裁法：让矩形一边在扇形的一半径OA上（图1）或让矩形一边与弦AB平行（图2）
（1）在图1中，设矩形一边PM的长为x，试把矩形PQRM的面积表示成关于x的函数；
（2）在图2中，设∠AOM=θ，试把矩形PQRM的面积表示成关于θ的函数；
（3）已知按图1的方案截得的矩形面积最大为
3
6
a2，那么请问哪种裁法能得到最大面积的矩形？说明理由．
（2012•辽宁）如图，已知椭圆C0：
x2
a2
+
y2
b2
=1(a＞b＞0，a，b为常数)，动圆C1：x2+y2=
t
2
1
，b＜t1＜a．点A1，A2分别为C0的左右顶点，C1与C0相交于A，B，C，D四点．
（I）求直线AA1与直线A2B交点M的轨迹方程；
（II）设动圆C2：x2+y2=
t
2
2
与C0相交于A'，B'，C'，D'四点，其中b＜t2＜a，t1≠t2．若矩形ABCD与矩形A'B'C'D'的面积相等，证明：
t
2
1
+
t
2
2
为定值．
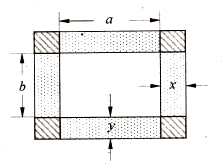（2012•江苏二模）如图，已知矩形油画的长为a，宽为b．在该矩形油画的四边镶金箔，四个角（图中斜线区域）装饰矩形木雕，制成一幅矩形壁画．设壁画的左右两边金箔的宽为x，上下两边金箔的宽为y，壁画的总面积为S．
（1）用x，y，a，b表示S；
（2）若S为定值，为节约金箔用量，应使四个矩形木雕的总面积最大．求四个矩形木雕总面积的最大值及对应的x，y的值．
精英家教网如图，已知矩形ABCD的边AB=2，BC=
2
，点E、F分别是边AB、CD的中点，沿AF、EC分别把三角形ADF和三角形EBC折起，使得点D和点B重合，记重合后的位置为点P．
（1）求证：平面PCE⊥平面PCF；
（2）设M、N分别为棱PA、EC的中点，求直线MN与平面PAE所成角的正弦；
（3）求二面角A-PE-C的大小．

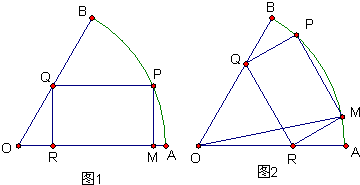
（本小题满分14分）如图，已知矩形ABCD的边AB="2" ,BC=,点E、F分别是边AB、CD的中点，沿AF、EC分别把三角形ADF和三角形EBC折起，使得点D和点B重合，记重合后的位置为点P。
(1)求证：平面PCE平面PCF；
(2)设M、N分别为棱PA、EC的中点，求直线MN与平面PAE所成角的正弦；
(3)求二面角A-PE-C的大小。
 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网