题目内容
三人独立破译同一份密码.已知三人各自破译出密码的概率分别为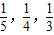 ,且他们是否破译出密码互不影响.
,且他们是否破译出密码互不影响.(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.
【答案】分析:根据题意,记“第i个人破译出密码”为事件A1(i=1,2,3),分析可得三个事件的概率且三个事件相互独立;
(Ⅰ)设“恰好二人破译出密码”为事件B,则B包括彼此互斥的A1•A2•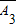 •A1•
•A1•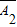 •A3+
•A3+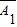 •A2•A3,由互斥事件的概率公式与独立事件的乘法公式计算可得答案;
•A2•A3,由互斥事件的概率公式与独立事件的乘法公式计算可得答案;
(Ⅱ)设“密码被破译”为事件C,“密码未被破译”为事件D,则D=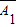 •
•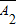 •
•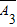 ,由独立事件的乘法公式计算可得D的概率,再由对立事件的概率公式可得C的概率,比较可得答案.
,由独立事件的乘法公式计算可得D的概率,再由对立事件的概率公式可得C的概率,比较可得答案.
解答:解:记“第i个人破译出密码”为事件A1(i=1,2,3),
依题意有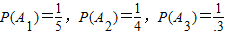 ,
,
且A1,A2,A3相互独立.
(Ⅰ)设“恰好二人破译出密码”为事件B,则有
B=A1•A2•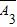 •A1•
•A1•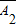 •A3+
•A3+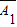 •A2•A3,
•A2•A3,
且A1•A2•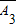 ,A1•
,A1•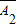 •A3,
•A3,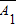 •A2•A3彼此互斥
•A2•A3彼此互斥
于是P(B)=P(A1•A2•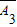 )+P(A1•
)+P(A1•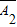 •A3)+P(
•A3)+P(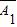 •A2•A3)
•A2•A3)
=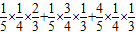
=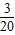 .
.
答:恰好二人破译出密码的概率为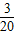 .
.
(Ⅱ)设“密码被破译”为事件C,“密码未被破译”为事件D.
D=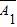 •
•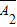 •
•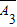 ,且
,且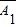 ,
,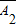 ,
,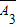 互相独立,则有
互相独立,则有
P(D)=P(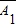 )•P(
)•P(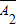 )•P(
)•P(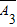 )=
)=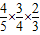 =
= .
.
而P(C)=1-P(D)= ,
,
故P(C)>P(D).
答:密码被破译的概率比密码未被破译的概率大.
点评:本题主要考查概率的基本知识与分类思想,考查运用数学知识分析问题、解决问题的能力,难点在于对于恰有二人破译出密码的事件分类不清.
(Ⅰ)设“恰好二人破译出密码”为事件B,则B包括彼此互斥的A1•A2•
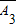 •A1•
•A1•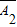 •A3+
•A3+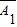 •A2•A3,由互斥事件的概率公式与独立事件的乘法公式计算可得答案;
•A2•A3,由互斥事件的概率公式与独立事件的乘法公式计算可得答案;(Ⅱ)设“密码被破译”为事件C,“密码未被破译”为事件D,则D=
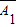 •
•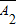 •
•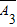 ,由独立事件的乘法公式计算可得D的概率,再由对立事件的概率公式可得C的概率,比较可得答案.
,由独立事件的乘法公式计算可得D的概率,再由对立事件的概率公式可得C的概率,比较可得答案.解答:解:记“第i个人破译出密码”为事件A1(i=1,2,3),
依题意有
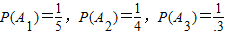 ,
,且A1,A2,A3相互独立.
(Ⅰ)设“恰好二人破译出密码”为事件B,则有
B=A1•A2•
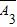 •A1•
•A1•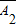 •A3+
•A3+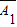 •A2•A3,
•A2•A3,且A1•A2•
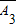 ,A1•
,A1•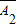 •A3,
•A3,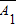 •A2•A3彼此互斥
•A2•A3彼此互斥于是P(B)=P(A1•A2•
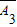 )+P(A1•
)+P(A1•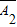 •A3)+P(
•A3)+P(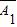 •A2•A3)
•A2•A3)=
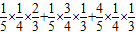
=
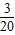 .
.答:恰好二人破译出密码的概率为
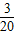 .
.(Ⅱ)设“密码被破译”为事件C,“密码未被破译”为事件D.
D=
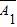 •
•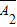 •
•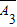 ,且
,且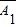 ,
,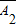 ,
,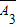 互相独立,则有
互相独立,则有P(D)=P(
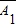 )•P(
)•P(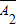 )•P(
)•P(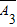 )=
)=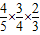 =
= .
.而P(C)=1-P(D)=
 ,
,故P(C)>P(D).
答:密码被破译的概率比密码未被破译的概率大.
点评:本题主要考查概率的基本知识与分类思想,考查运用数学知识分析问题、解决问题的能力,难点在于对于恰有二人破译出密码的事件分类不清.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
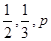 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为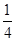 .
.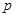 的值;
的值;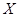 ,求
,求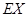 .
.