题目内容
已知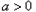
，函数
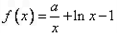（其中e为自然对数的底数）．
（Ⅰ）求函数f(x)在区间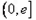
上的最小值；
（Ⅱ）设数列{an}的通项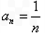
，Sn是前n项和，证明：
．
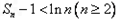（Ⅰ）解：求导函数，令其等于0，即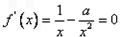
，可得x=a
若a≥e时，函数f（x）在区间（0，e]是减函数，
∴f（x）min=f（e）=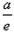
；
0＜a＜e时，函数f（x）在区间（0，a]是减函数，[a，e]是增函数，
∴f（x）min=f（a）=lna；
（Ⅱ）证明：由（Ⅰ）可知，a=1时，函数f（x）在定义域的最小值为0，
∴lnx＞1-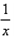
在[1，+∞）上成立
令x=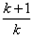
得 ln（k+1）-lnk＞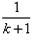
令k=1，2，3，…，（n-1），
可得ln2-ln1＞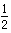
，ln3-ln2＞
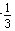，…，lnn-ln（n-1）＞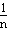
∵数列{an}的通项an=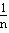
，Sn是前n项和，
∴叠加，可得Sn-1＜lnn（n≥2）
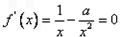，可得x=a 若a≥e时，函数f（x）在区间（0，e]是减函数，
∴f（x）min=f（e）=
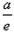；0＜a＜e时，函数f（x）在区间（0，a]是减函数，[a，e]是增函数，
∴f（x）min=f（a）=lna；
（Ⅱ）证明：由（Ⅰ）可知，a=1时，函数f（x）在定义域的最小值为0，
∴lnx＞1-
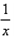在[1，+∞）上成立令x=
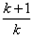得 ln（k+1）-lnk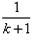＞令k=1，2，3，…，（n-1），
可得ln2-ln1＞
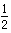，ln3-ln2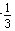＞ ，…，lnn-ln（n-1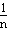）＞∵数列{an}的通项an=
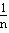，Sn是前n项和，∴叠加，可得Sn-1＜lnn（n≥2）
练习册系列答案
相关题目
（其中e为自然对数）
的极值。
（常数a>0），当x>1时，求函数G(x)的单调区
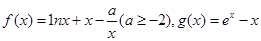，其中e为自然对数的底数，且当x>0时
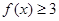恒成立．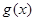
的单调区间；
.
（其中e为自然对数）
的极值。
（常数a>0），当x>1时，求函数G(x)的单调区间，并在极值存在处求极值。
.（其中e为自然对数的底数，e=2.71828…〉.
时，求函数
的图象在点
处的切线方程；
时，试求函数
，则当
时，函数
所表示的平面区域内，请写出判断过程.