题目内容
已知：函数
.（其中e为自然对数的底数，e=2.71828…〉.
(1)
当
时，求函数
的图象在点
处的切线方程；
(2)
当
时，试求函数的极值；
(3)若
，则当
时，函数的图象是否总在不等式
所表示的平面区域内，请写出判断过程.
【答案】
解析：
（1）
所以，当
时函数
的图象在点
处的切线的斜率为1
故所求切线方程为
……………………..2分
（2）当
时
恒成立，函数定义域为R
又
单调递增，
单调递减，
单调递增
所以函数的极大值为
，极大值为
…………………..5分
（3）①当时
法一：因为函数在
单调递增，所以其最小值为
，而函数在的最大值为1，所以函数图象总在不等式
所表示的平面区域内……………..6分
法二：因为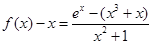
而当
时
，
又，
，即当
时
成立
所以函数图象总在不等式所表示的平面区域内……………..6分
②当
时，
法一：仿上可得函数在上时，上述结论仍然成立……………..7分
法二：因为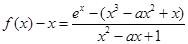
，由（2）知
而当时
又，
，即当时成立……………..7分
而当
时，因为函数递减，其最小值为
所以，下面判断
的关系，即判断
的关系，
令
单调递增
使得
上单调递减，在
单调递增……………………………..10分
所以
即
也即
所以函数图象总在不等式所表示的平面区域内……………..12分
【解析】略
练习册系列答案
相关题目
”是“
”的充分不必要条件；
的反函数为
其中x>-1；
是函数
的导函数，若
=0，则
必为函数的极值点；
万人
”是“
”的充分不必要条件；
的反函数为
其中x>-1；
是函数
的导函数，若
=0，则
必为函数的极值点；
万人