题目内容
判断正误:用反正切函数表示.
arccot(-![]() )=π-arctan
)=π-arctan![]() .
.
( )
答案:T
解析:
解析:
|
解: 令α=arccot(- tanα=- ∵ (α-π)在反正切函数的取值区间上. ∵tanα=tan(α-π)=- ∴α-π=arctan(- 即arccot(- |

练习册系列答案
相关题目
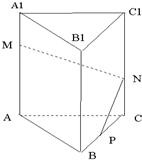 如图,在正三棱柱ABC-A1B1C1中,AB=3,AA1=6,M为AA1上的点,且AM=2MA1,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M点的最短路线长为
如图,在正三棱柱ABC-A1B1C1中,AB=3,AA1=6,M为AA1上的点,且AM=2MA1,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M点的最短路线长为