ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊдВC1ЃКЃЈx+1ЃЉ2+y2=1ЃЌдВC2ЃКЃЈxЉ3ЃЉ2+ЃЈyЉ4ЃЉ2=1ЃЎ
ЃЈЂёЃЉШєЙ§ЕуC1ЃЈЉ1ЃЌ0ЃЉЕФжБЯпlБЛдВC2НиЕУЕФЯвГЄЮЊ ![]() ЃЌЧѓжБЯпlЕФЗНГЬЃЛ
ЃЌЧѓжБЯпlЕФЗНГЬЃЛ
ЃЈЂђЃЉдВDЪЧвд1ЮЊАыОЖЃЌдВаФдкдВC3ЃКЃЈx+1ЃЉ2+y2=9ЩЯвЦЖЏЕФЖЏдВЃЌШєдВDЩЯШЮвтвЛЕуPЗжБ№зїдВC1ЕФСНЬѕЧаЯпPEЃЌPFЃЌЧаЕуЮЊEЃЌFЃЌЧѓ ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂѓЃЉШєЖЏдВCЭЌЪБЦНЗждВC1ЕФжмГЄЁЂдВC2ЕФжмГЄЃЌдђЖЏдВCЪЧЗёОЙ§ЖЈЕуЃПШєОЙ§ЃЌЧѓГіЖЈЕуЕФзјБъЃЛШєВЛОЙ§ЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПНтЃКЃЈЂёЃЉЩшжБЯпlЕФЗНГЬЮЊy=kЃЈ+1ЃЉЃЌМДkxЉy+k=0ЃЎ
вђЮЊжБЯпlБЛдВC2НиЕУЕФЯвГЄЮЊ ![]() ЃЌЖјдВC2ЕФАыОЖЮЊ1ЃЌ
ЃЌЖјдВC2ЕФАыОЖЮЊ1ЃЌ
ЫљвддВаФC2ЃЈ3ЃЌ4ЃЉЕНlЃКkxЉy+k=0ЕФОрРыЮЊ ![]() ЃЎ
ЃЎ
ЛЏМђЃЌЕУ12k2Љ25k+12=0ЃЌНтЕУk= ![]() Лђk=
Лђk= ![]() ЃЎ
ЃЎ
ЫљвджБЯпlЗНГЬЮЊ4xЉ3y+4=0Лђ3xЉ4y+3=0
ЃЈЂђЃЉЖЏдВDЪЧдВаФдкЖЈдВЃЈx+1ЃЉ2+y2=9ЩЯвЦЖЏЃЌАыОЖЮЊ1ЕФдВ
ЩшЁЯEC1F=2ІСЃЌдђдкRtЁїPC1EжаЃЌ ![]() ЃЌ
ЃЌ
га ![]() ЃЌ
ЃЌ
дђ ![]()
гЩдВЕФМИКЮаджЪЕУЃЌ|DC1|ЉrЁм|PC1|Ём|DC1|+rЃЌМД2Ём|PC1|Ём4ЃЌ ![]()
дђ ![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ ![]() ЃЌзюаЁжЕЮЊ
ЃЌзюаЁжЕЮЊ ![]() ЃЎ
ЃЎ
ЙЪ ![]() ЃЎ
ЃЎ
ЃЈЂѓЃЉЩшдВаФCЃЈxЃЌyЃЉЃЌгЩЬтвтЃЌЕУCC1=CC2 ЃЌ
МД ![]() ЃЎ
ЃЎ
ЛЏМђЕУx+yЉ3=0ЃЌМДЖЏдВдВаФCдкЖЈжБЯпx+yЉ3=0ЩЯдЫЖЏЃЎ
ЩшCЃЈm.3ЉmЃЉЃЌдђЖЏдВCЕФАыОЖЮЊ ![]() =
= ![]() ЃЎ
ЃЎ
гкЪЧЖЏдВCЕФЗНГЬЮЊЃЈxЉmЃЉ2+ЃЈyЉ3+mЃЉ2=1+ЃЈm+1ЃЉ2+ЃЈ3ЉmЃЉ2 ЃЎ
ећРэЃЌЕУx2+y2Љ6yЉ2Љ2mЃЈxЉy+1ЃЉ=0ЃЎ
гЩ ![]() ЕУ
ЕУ 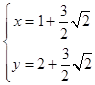 Лђ
Лђ 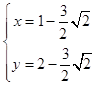
ЫљвдЖЈЕуЕФзјБъЮЊЃЈ1Љ ![]() ЃЌ2Љ
ЃЌ2Љ ![]() ЃЉЃЌЃЈ1+
ЃЉЃЌЃЈ1+ ![]() ЃЌ2+
ЃЌ2+ ![]() ЃЉ
ЃЉ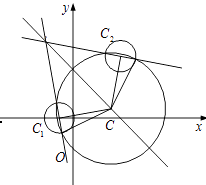

ЁОНтЮіЁПЃЈЂёЃЉЩшжБЯпlЕФЗНГЬЮЊy=kЃЈ+1ЃЉЃЌИљОнжБЯпlБЛдВC2НиЕУЕФЯвГЄЮЊ ![]() ЃЌРћгУЙДЙЩЖЈРэЃЌЧѓГіkЃЌМДПЩЧѓжБЯпlЕФЗНГЬЃЛЃЈЂђЃЉЖЏдВDЪЧдВаФдкЖЈдВЃЈx+1ЃЉ2+y2=9ЩЯвЦЖЏЃЌАыОЖЮЊ1ЕФдВЃЌгЩдВЕФМИКЮаджЪЕУЃЌ|DC1|ЉrЁм|PC1|Ём|DC1|+rЃЌМД2Ём|PC1|Ём4ЃЌ
ЃЌРћгУЙДЙЩЖЈРэЃЌЧѓГіkЃЌМДПЩЧѓжБЯпlЕФЗНГЬЃЛЃЈЂђЃЉЖЏдВDЪЧдВаФдкЖЈдВЃЈx+1ЃЉ2+y2=9ЩЯвЦЖЏЃЌАыОЖЮЊ1ЕФдВЃЌгЩдВЕФМИКЮаджЪЕУЃЌ|DC1|ЉrЁм|PC1|Ём|DC1|+rЃЌМД2Ём|PC1|Ём4ЃЌ ![]() ЃЌРћгУЯђСПЕФЪ§СПЛ§ЙЋЪНЃЌМДПЩЧѓ
ЃЌРћгУЯђСПЕФЪ§СПЛ§ЙЋЪНЃЌМДПЩЧѓ ![]() ЕФШЁжЕЗЖЮЇЃЛЃЈЂѓЃЉШЗЖЈЖЏдВдВаФCдкЖЈжБЯпx+yЉ3=0ЩЯдЫЖЏЃЌЧѓГіЖЏдВCЕФЗНГЬЃЌМДПЩЕУГіНсТлЃЎ
ЕФШЁжЕЗЖЮЇЃЛЃЈЂѓЃЉШЗЖЈЖЏдВдВаФCдкЖЈжБЯпx+yЉ3=0ЩЯдЫЖЏЃЌЧѓГіЖЏдВCЕФЗНГЬЃЌМДПЩЕУГіНсТлЃЎ

ЁОЬтФПЁПМйЩшЙигкФГЩшБИЕФЪЙгУФъЯоxКЭЫљжЇГіЕФЮЌаоЗбгУyЃЈЭђдЊЃЉЃЌгаШчЯТЕФЭГМЦзЪСЯЃК
x | 1 | 2 | 3 | 4 | 5 |
y | 5 | 6 | 7 | 8 | 10 |
гЩзЪСЯПЩжЊyЖдxГЪЯпадЯрЙиЙиЯЕЃЌЧвЯпадЛиЙщЗНГЬЮЊ ![]() ЃЌЧыЙРМЦЪЙгУФъЯоЮЊ20ФъЪБЃЌЮЌаоЗбгУдМЮЊЃЈ ЃЉ
ЃЌЧыЙРМЦЪЙгУФъЯоЮЊ20ФъЪБЃЌЮЌаоЗбгУдМЮЊЃЈ ЃЉ
A.26.2
B.27
C.27.6
D.28.2