题目内容
10．已知函数f（x）=x|m-x|（x∈R），且f（4）=0．（1）求实数m的值；
（2）作出函数f（x）的图象并判断其零点个数；
（3）根据图象指出f（x）的单调递减区间；
（4）根据图象写出不等式f（x）＞0的解集；
（5）求集合M={m|使方程f（x）=m有三个不相等的实根}．
分析 由题意知f（4）=4|m-4|=0，从而解出f（x）=x|4-x|，作函数的图象，由图象写出函数的性质即可．
解答 解：（1）f（4）=4|m-4|=0，故m=4；
（2）作函数f（x）=x|4-x|的图象如下，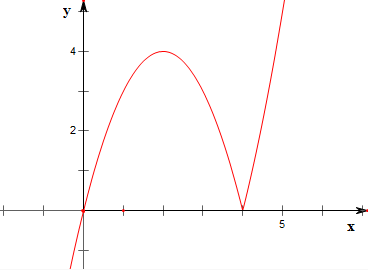
结合函数的图象可知，其有两个零点；
（3）由图象可知，f（x）的单调递减区间为（2，4）；
（4）由图象可知，不等式f（x）＞0的解集为（0，4）∪（4，+∞）；
（5）由图象可知，集合M={m|使方程f（x）=m有三个不相等的实根}
=（0，4）．
点评 本题考查了学生的作图能力及应用图象的能力．
练习册系列答案
相关题目
20．函数y=ax2+bx+c（a≠0）的函数值均为正数，那么（ ）
| A． | a＞0，△＜0 | B． | a＜0，△≤0 | C． | a＞0，△≥0 | D． | a＞0，△＞0 |
18．若f（x）=ax2-$\sqrt{2}$（a＞0），且f（$\sqrt{2}$）=2，则a等于（ ）
| A． | 1+$\frac{\sqrt{2}}{2}$ | B． | 1-$\frac{\sqrt{2}}{2}$ | C． | 0 | D． | 2 |
如图：下面三个分别是y=1og2x，y=${log}_{\frac{1}{3}}x$，y=log${\;}_{\frac{1}{4}}$x函数图象，则A代表函数y=1og2x； B代表函数y=log${\;}_{\frac{1}{4}}$x； C代表函数y=1og$\frac{1}{3}$x．