题目内容
对于任意的实数a,不等式|a+1|+|a-1|≥M恒成立,记实数M的最大值是m.
(1)求m的值;
(2)解不等式|x-1|+|2x-3|≤m.
(1)求m的值;
(2)解不等式|x-1|+|2x-3|≤m.
(1)由绝对值不等式,有|a+1|+|a-1|≥|(a+1)-(a-1)|=2,
那么对于|a+1|+|a-1|≥M,只需|a+1|+|a-1|min≥M,即M≤2,则m=2.
(2)不等式即|x-1|+|2x-3|≤2,
当x≤1时:1-x-2x+3≤2,即x≥
,则
≤x≤1,
当1<x<
时:x-1-2x+3≤2,即x≥0,则1<x<
,
当x≥
时:x-1+2x-3≤2,即x≤3,则
≤x≤3,
那么不等式的解集为[
,1]∪(1,
)∪[
,3]=[
,3].
那么对于|a+1|+|a-1|≥M,只需|a+1|+|a-1|min≥M,即M≤2,则m=2.
(2)不等式即|x-1|+|2x-3|≤2,
当x≤1时:1-x-2x+3≤2,即x≥
| 2 |
| 3 |
| 2 |
| 3 |
当1<x<
| 3 |
| 2 |
| 3 |
| 2 |
当x≥
| 3 |
| 2 |
| 3 |
| 2 |
那么不等式的解集为[
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |

练习册系列答案
相关题目
设函数f(x)=x+ln(x+
),则对于任意的实数a和b,a+b<0是f(a)+f(b)<0的( )
| 1+x2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分且必要条件 |
| D、既不充分又不必要条件 |
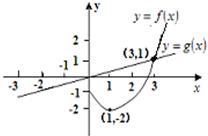 对于任意的实数a,b,记max{a,b}=
对于任意的实数a,b,记max{a,b}=
|
| A、y=F(x)为奇函数 |
| B、y=F(x)在(-3,0)上为增函数 |
| C、y=F(x)的最小值为-2,最大值为2 |
| D、以上说法都不正确 |
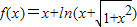 ,则对于任意的实数a和b,a+b<0是f(a)+f(b)<0的( )
,则对于任意的实数a和b,a+b<0是f(a)+f(b)<0的( )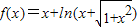 ,则对于任意的实数a和b,a+b<0是f(a)+f(b)<0的( )
,则对于任意的实数a和b,a+b<0是f(a)+f(b)<0的( ) ,则对于任意的实数a和b,a+b<0是f(a)+f(b)<0的( )
,则对于任意的实数a和b,a+b<0是f(a)+f(b)<0的( )