题目内容
设函数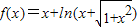
，则对于任意的实数a和b，a+b＜0是f（a）+f（b）＜0的（ ）A．必要不充分条件
B．充分不必要条件
C．充分且必要条件
D．既不充分又不必要条件
【答案】分析：由题设条件知对于任意的实数a和b，a+b＜0⇒f（a）+f（b）＜0；f（a）+f（b）＜0⇒a+b＜0．
解答：解：显然，函数
在R上是递增函数，
而且是奇函数，于是，由a+b＜0，得a＜-b，有f（a）＜f（-b）=-f（b），
即f（a）+f（b）＜0．反过来，也成立．
故选C．
点评：本题考查充分条件、必要条件、充要条件的判断，解题时要注意函数单调性的合理运用．
解答：解：显然，函数
在R上是递增函数，而且是奇函数，于是，由a+b＜0，得a＜-b，有f（a）＜f（-b）=-f（b），
即f（a）+f（b）＜0．反过来，也成立．
故选C．
点评：本题考查充分条件、必要条件、充要条件的判断，解题时要注意函数单调性的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
，则对于任意的实数
和
，
是
的（ ）
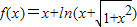，则对于任意的实数a和b，a+b＜0是f（a）+f（b）＜0的（ ）
，则对于任意的实数a和b，a+b＜0是f（a）+f（b）＜0的（ ）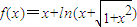
，则对于任意的实数a和b，a+b＜0是f（a）+f（b）＜0的（ ）