题目内容
设集合A为函数y=ln(-x2-2x+8)的定义域,集合B为函数y=x+
的值域,集合C为不等式(ax-
)(x+4)≤0的解集.
(1)求A∩B;
(2)若C⊆CRA,求a的取值范围.
| 1 |
| x+1 |
| 1 |
| a |
(1)求A∩B;
(2)若C⊆CRA,求a的取值范围.
(1)∵-x2-2x+8>0,
∴解得A=(-4,2).
∵y=x+
,
∴B=(-∞,-3]∪[1,+∞);
所以A∩B=(-4,-3]∪[1,2);
(2)∵CRA=(-∞,-4]∪[2,+∞),C⊆CRA,
若a<0,则不等式(ax-
)(x+4)≤0的解集只能是(-∞,-4]∪[
,+∞),故定有
≥2得a2≤
解得-
≤a<0
若a>0,则不等式(ax-
)(x+4)≤0的解集只能是∅
∴a的范围为-
≤a<0.
∴解得A=(-4,2).
∵y=x+
| 1 |
| x+1 |
∴B=(-∞,-3]∪[1,+∞);
所以A∩B=(-4,-3]∪[1,2);
(2)∵CRA=(-∞,-4]∪[2,+∞),C⊆CRA,
若a<0,则不等式(ax-
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| 2 |
| ||
| 2 |
若a>0,则不等式(ax-
| 1 |
| a |
∴a的范围为-
| ||
| 2 |

练习册系列答案
相关题目
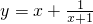 的值域,集合C为不等式
的值域,集合C为不等式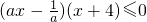 的解集.
的解集. 的值域,集合C为不等式(ax-
的值域,集合C为不等式(ax- )(x+4)≤0的解集.
)(x+4)≤0的解集. CRA,求a的取值范围.
CRA,求a的取值范围.