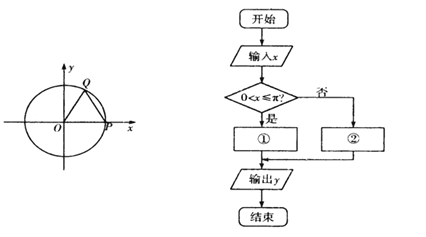
题目内容
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρsin(θ+ ![]() )=
)= ![]() .圆O的参数方程为
.圆O的参数方程为  (θ为参数,r>0).
(θ为参数,r>0).
(Ⅰ)求圆O的圆心的极坐标(ρ≥0,0≤θ<2π );
(Ⅱ)当r为何值时,圆O上的点到直线l的最大距离为2+ ![]() .
.
【答案】解:(Ⅰ)圆O的参数方程为 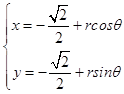 , 可得圆心为(
, 可得圆心为( ![]() ),
),
由ρ2=x2+y2 , 可得ρ=1,tanθ= ![]() =
= ![]() .
.
∴圆心的极坐标为(1, ![]() ).
).
(Ⅱ)直线l的极坐标方程ρsin(θ+ ![]() )=
)= ![]() 化为普通方程,可得
化为普通方程,可得 ![]() ρsinθ+
ρsinθ+ ![]() ρcosθ=
ρcosθ= ![]() ,即x+y﹣1=0,
,即x+y﹣1=0,
把参数方程 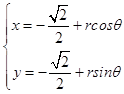 ,
,
由圆心到直线的距离公式d= 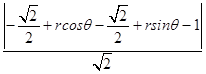 ,即d=
,即d= 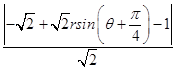 ,
,
当sin( ![]() )=﹣1时,圆O上的点到直线l的最大,即
)=﹣1时,圆O上的点到直线l的最大,即 ![]() =2+
=2+ ![]() ,
,
解得r=1
∴当r=1时,圆O上的点到直线l的最大距离为2+ ![]()
【解析】(Ⅰ)根据圆O的参数方程为 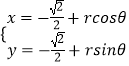 可得圆心为(
可得圆心为( ![]() ),根据ρ2=x2+y2 , 可得ρ=1,tanθ=
),根据ρ2=x2+y2 , 可得ρ=1,tanθ= ![]() =
= ![]() .可得圆心的极坐标.(Ⅱ)将直线l的极坐标方程ρsin(θ+
.可得圆心的极坐标.(Ⅱ)将直线l的极坐标方程ρsin(θ+ ![]() )=
)= ![]() 化为普通方程,然后把参数方程
化为普通方程,然后把参数方程 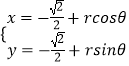 带入圆心到直线的距离公式d,利用三角函数的有界限即可求.
带入圆心到直线的距离公式d,利用三角函数的有界限即可求.

【题目】某服装批发市场1-5月份的服装销售量![]() 与利润
与利润![]() 的统计数据如下表:
的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销售量 | 3 | 6 | 4 | 7 | 8 |
利润 | 19 | 34 | 26 | 41 | 46 |
(1)从这五个月的利润中任选2个,分别记为![]() ,
, ![]() ,求事件“
,求事件“![]() ,
, ![]() 均不小于30”的概率;
均不小于30”的概率;
(2)已知销售量![]() 与利润
与利润![]() 大致满足线性相关关系,请根据前4个月的数据,求出
大致满足线性相关关系,请根据前4个月的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的利润的估计数据与真实数据的误差不超过2万元,则认为得到的利润的估计数据是理想的.请用表格中第5个月的数据检验由(2)中回归方程所得的第5个月的利润的估计数据是否理想.参考公式:  .
.