��Ŀ����
����Ŀ��Ͳ�����ҹ��Ŵ�������һ��ˮ����ȹ��ߣ�������ѧ��������ڡ�ũ��ȫ�顷����ͼ�������Ͳ���Ĺ���ԭ������ͼ1�������侭���ֻ�����������ũҵ�����еõ�ʹ�ã���ͼ2�����ٶ���ˮ�����ȶ�������£�Ͳ���ϵ�ÿһ��ʢˮͲ��������Բ���˶�����Ͳ����ʢˮͲ���˶����������ԣ����Կ����������Ǻ���ģ�Ϳ̻�ʢˮͲ����Ϊ�ʵ㣩���˶����ɣ���Ͳ������Ϊһ������ͼ�Σ�����ֱ������ϵ����ͼ3�����辭��t���Ͳ���ϵ�ij��ʢˮͲ![]() �ӵ�P0�˶�����P����Ͳ���Ĺ���ԭ����֪�����ʢˮͲ����ˮ��ĸ߶�H(��λ:
�ӵ�P0�˶�����P����Ͳ���Ĺ���ԭ����֪�����ʢˮͲ����ˮ��ĸ߶�H(��λ: ![]() )������������������Ͳ��ת�ֵ�����O��ˮ��ľ���h��Ͳ���İ뾶r��Ͳ��ת���Ľ��ٶ�������λ:
)������������������Ͳ��ת�ֵ�����O��ˮ��ľ���h��Ͳ���İ뾶r��Ͳ��ת���Ľ��ٶ�������λ: ![]() ����ʢˮͲ�ij�ʼλ��P0�Լ���������ʱ��t(��λ:
����ʢˮͲ�ij�ʼλ��P0�Լ���������ʱ��t(��λ:![]() )����֪r=3
)����֪r=3![]() ��h=2
��h=2![]() ��Ͳ��ÿ����ת��(����ʱ�뷽��)1.5Ȧ�� ��P0����ˮ��ĸ߶�Ϊ3.5
��Ͳ��ÿ����ת��(����ʱ�뷽��)1.5Ȧ�� ��P0����ˮ��ĸ߶�Ϊ3.5![]() ����ʢˮͲM�ӵ�P0��ʼ����ʱ�䣬��������Ҫ����_______
����ʢˮͲM�ӵ�P0��ʼ����ʱ�䣬��������Ҫ����_______![]() �Ϳɵ�����ߵ㣻������
�Ϳɵ�����ߵ㣻������![]() ����ˮ��ĸ߶�
����ˮ��ĸ߶�![]() ��ʾΪʱ��
��ʾΪʱ��![]() �ĺ�������˺�������ʽΪ_________��
�ĺ�������˺�������ʽΪ_________��



ͼ1 ͼ2 ͼ3
���𰸡�![]()
![]()
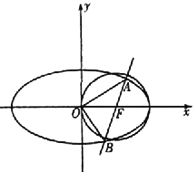
��������
���������������ʼλ��![]() ��
��![]() �Ǹ�����ļнǣ���
�Ǹ�����ļнǣ���![]() ��һ�ε�����ߵ�ʱ�������ת���Ļ��ȣ�����Ͳ��ÿ����ת���Ļ��ȣ������һ�ε�����ߵ��ʱ�䣬���ɵó���һ�գ�
��һ�ε�����ߵ�ʱ�������ת���Ļ��ȣ�����Ͳ��ÿ����ת���Ļ��ȣ������һ�ε�����ߵ��ʱ�䣬���ɵó���һ�գ�
�����Ǻ����Ķ���ó�����![]() �������꣬���������������
�������꣬���������������![]() ����ˮ��ĸ߶�
����ˮ��ĸ߶�![]() �����ɵó��ڶ���.
�����ɵó��ڶ���.
��Ϊ��P0����ˮ��ĸ߶�Ϊ3.5![]() ����ʼʱ
����ʼʱ![]() ��
��![]() �Ǹ�����ļн�Ϊ
�Ǹ�����ļн�Ϊ![]()
�������֪��Ͳ��ÿ����ת��(����ʱ�뷽��)![]() ����Ͳ��ÿ����ת��
����Ͳ��ÿ����ת��![]()
��![]() ��һ�ε�����ߵ�ʱ����ת���Ļ���Ϊ
��һ�ε�����ߵ�ʱ����ת���Ļ���Ϊ![]() ��������ʱ��Ϊ
��������ʱ��Ϊ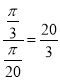
����ʢˮͲM�ӵ�P0��ʼ����ʱ�䣬��������Ҫ����![]()
![]() �Ϳɵ�����ߵ㣻
�Ϳɵ�����ߵ㣻
��![]() ��
��![]() �Ǹ�����ļн�Ϊ
�Ǹ�����ļн�Ϊ![]() ����
����![]()
�����Ǻ����Ķ����֪��![]() ��������Ϊ
��������Ϊ![]() ��
��![]()
���![]() ����ˮ��ĸ߶�
����ˮ��ĸ߶�![]() �ĺ���Ϊ
�ĺ���Ϊ![]() ��
��![]()
�ʴ�Ϊ��![]() ��
��![]()

 53������ϵ�д�
53������ϵ�д�