Question

【题目】如图，在三棱柱ABC中，侧面是矩形，∠BAC=90°，⊥BC，=AC=2AB=4，且⊥．

(1)求证：平面⊥平面；

(2)设D是的中点，判断并证明在线段上是否存在点E，使得DE∥平面．若存在，求二面角EB的余弦值．

Answer 1

【答案】（1）见解析；（2）.

【解析】分析：（1）易知⊥平面ABC，有⊥AC，依次可证得⊥，⊥，从而得证；

（2）当E为的中点时，连接AE，，DE，易证得平面EFD∥平面，以 A为坐标原点，AB，AC，所在的直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系，分别求面和面的法向量，由法向量的夹角可求二面角的余弦值.

详解：(1)在三棱柱ABC中，侧面是矩形，∴⊥AB，

又⊥BC，AB∩BC=B，

∴⊥平面ABC，∴⊥AC.

又=AC，∴⊥．

又⊥，∩=，

∴⊥平面 ，

又 平面，∴平面⊥平面．

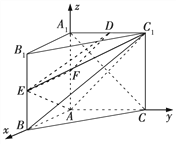
图1

(2)解法一　当E为的中点时，连接AE，，DE，如图1，取的中点F，连接EF，FD，

∵EF∥AB，DF∥，

又EF∩DF=F，AB∩=A，

∴平面EFD∥平面，

则有DE∥平面．

以 A为坐标原点，AB，AC，所在的直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系，因为=AC=2AB=4，

∴A(0，0，0)，B(2，0，0)，(0，4，4)，C(0，4，0)，E(2，0，2)，(0，0，4)，由(1)知，=(0，4，4)是平面的一个法向量．

设n=(x，y，z)为平面的法向量，

∵=(0，4，4)，=(2，0，2)，

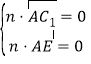
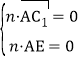∴ ，即 ，

令z=1，则x=1，y=1，

∴n=(1，1，1)为平面的一个法向量．

设 与n的夹角为θ，则cos θ== ，由图知二面角EB为锐角，∴二面角EB的余弦值为 ．

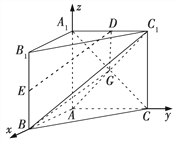
图2

解法二　当E为的中点时，连接DE，如图2，设交于点G，连接BG，DG，∵BEDG，∴四边形DEBG为平行四边形，

则DE∥BG，又DE平面，BG平面，则DE∥平面．

求二面角EB的余弦值同解法一．