题目内容
函数f（x）定义域为R+，对任意x，y∈R+都有f（xy）=f（x）+f（y），又f（8）=3，则f（
）=（ ）A．
B．1
C．-
D．
【答案】分析：根据函数f（x）定义域为R+，对任意x，y∈R+都有f（xy）=f（x）+f（y），可把f（8）逐步变形，最后用f（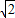
）
表示，就可求出f（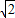
）的值．
解答：解：∵函数f（x），对任意x，y∈R+都有f（xy）=f（x）+f（y），
∴且f（8）=f（2）+f（4）=f（2）+f（2）+f（2）=3f（2）=6f（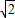
）=3
∴f（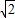
）=
故选A
点评：本题考查了抽象函数的性质，做题时要善于发现规律．
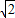）表示，就可求出f（
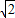）的值．解答：解：∵函数f（x），对任意x，y∈R+都有f（xy）=f（x）+f（y），
∴且f（8）=f（2）+f（4）=f（2）+f（2）+f（2）=3f（2）=6f（
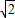）=3∴f（
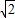）=故选A
点评：本题考查了抽象函数的性质，做题时要善于发现规律．
练习册系列答案
相关题目