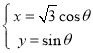题目内容
【题目】在平面直角坐标系![]() 中,直线
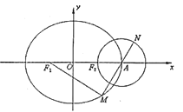
中,直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数
为参数![]() ),以原点为极点,
),以原点为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的焦点的极坐标;
的焦点的极坐标;
(2)若曲线![]() 的上焦点为
的上焦点为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,求直线
,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)用二倍角公式化简![]() ,将
,将![]() 代入曲线
代入曲线![]() 方程,求出曲线
方程,求出曲线![]() 的直角坐标方程,进而求出焦点坐标,再化为极坐标;
的直角坐标方程,进而求出焦点坐标,再化为极坐标;
(2)将直线![]() 方程与曲线
方程与曲线![]() 方程联立,由根与系数关系结合直线参数的几何意义,求出关于
方程联立,由根与系数关系结合直线参数的几何意义,求出关于![]() 的关系式,即可求解.
的关系式,即可求解.
(1)由![]() ,
,
得![]() ,
,
∴![]() ,
,
即![]() .
.
∴曲线![]() 是焦点在
是焦点在![]() 轴上的椭圆,焦点坐标为
轴上的椭圆,焦点坐标为![]() ,
,
则焦点的极坐标为![]() ,
,![]() ;
;
(2)将直线![]() 的参数方程
的参数方程![]()
(其中![]() 为参数,
为参数,![]() )代入
)代入![]() ,
,
得![]() ,
,
整理得:![]() .
.
∵![]() ,
,
∴![]() 与
与![]() 异号,
异号,
则![]() ,
,
即![]() ,
,![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() ,即直线
,即直线![]() 的斜率为
的斜率为![]() .
.

【题目】下表给出的是某城市![]() 年至
年至![]() 年,人均存款
年,人均存款![]() (万元),人均消费
(万元),人均消费![]() (万元)的几组对照数据.
(万元)的几组对照数据.
年份 |
|
|
|
|
人均存款 |
|
|
|
|
人均消费 |
|
|
|
|
(1)试建立![]() 关于
关于![]() 的线性回归方程;如果该城市
的线性回归方程;如果该城市![]() 年的人均存款为
年的人均存款为![]() 万元,请根据线性回归方程预测
万元,请根据线性回归方程预测![]() 年该城市的人均消费;
年该城市的人均消费;
(2)计算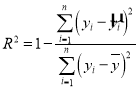 ,并说明线性回归方程的拟合效果.
,并说明线性回归方程的拟合效果.
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为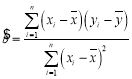 ,
,![]() .
.
【题目】由国家统计局提供的数据可知,2012年至2018年中国居民人均可支配收入![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均可支配收入 | 1.65 | 1.83 | 2.01 | 2.19 | 2.38 | 2.59 | 2.82 |
(1)求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)利用(1)中的回归方程,分析2012年至2018年中国居民人均可支配收入的变化情况,并预测2019年中国居民人均可支配收入.
附注:参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: 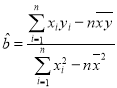 ,
,![]() .
.