题目内容
已知O为直二面角α-MN-β的棱MN上的一点，射线OE，OF分别在α，β内，并且∠EON=∠FON=45°，则∠EOF的大小为________．
60°
分析：过棱ON上一点C分别在α，β平面内作棱的垂线CA，CB，连接AB，利用∠EON=∠FON=45°，可计算OA，OB的长，利用α-MN-β为直二面角，可计算AB的长，从而问题可解．
解答：过棱ON上一点C分别在α，β平面内作棱的垂线CA，CB，连接AB
不妨假设OC=1，
则∵∠EON=∠FON=45°，∴OA=OB=2
∵α-MN-β为直二面角，∴AB=2
∴∠AOB=60°
即∠EOF=60°
故答案为：60°．
点评：本题的考点是与二面角有关的立体几何综合题，主要考查计算线线角，关键是寻找二面角的平面角，利用直角三角形研究边的关系，属于基础题．
分析：过棱ON上一点C分别在α，β平面内作棱的垂线CA，CB，连接AB，利用∠EON=∠FON=45°，可计算OA，OB的长，利用α-MN-β为直二面角，可计算AB的长，从而问题可解．
解答：过棱ON上一点C分别在α，β平面内作棱的垂线CA，CB，连接AB
不妨假设OC=1，
则∵∠EON=∠FON=45°，∴OA=OB=2
∵α-MN-β为直二面角，∴AB=2
∴∠AOB=60°
即∠EOF=60°
故答案为：60°．
点评：本题的考点是与二面角有关的立体几何综合题，主要考查计算线线角，关键是寻找二面角的平面角，利用直角三角形研究边的关系，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
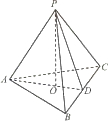如图，在三棱锥P-ABC中，AB=AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上，已知BC=8，PO=4，AO=3，OD=2
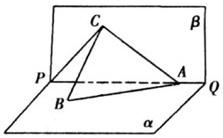如图所示，PQ为平面α、β的交线，已知二面角α-PQ-β为直二面角，A∈PQ，B∈α，C∈β，CA=CB=kAB（k∈R*），∠BAP=45°．