题目内容
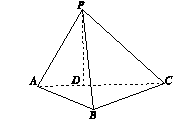
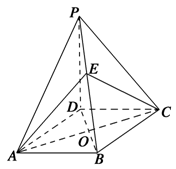
如图所示,四棱锥P—ABCD中,AB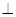 AD,CD
AD,CD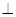 AD,PA
AD,PA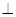 底面ABCD,PA=AD=CD=2AB=2,M为PC的中点。
底面ABCD,PA=AD=CD=2AB=2,M为PC的中点。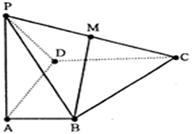
(1)求证:BM∥平面PAD;
(2)在侧面PAD内找一点N,使MN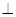 平面PBD;
平面PBD;
(3)求直线PC与平面PBD所成角的正弦。
(1)详见解析,(2)详见解析,(3)
解析试题分析:(1)证明线面平行,往往从线线平行出发. 因为 是
是 的中点,所以取PD的中点
的中点,所以取PD的中点 ,则ME为三角形PCD的中位线,根据中位线的性质,有
,则ME为三角形PCD的中位线,根据中位线的性质,有

 ,又
,又

 ,所以四边形
,所以四边形 为平行四边形,因此
为平行四边形,因此 ∥
∥ ,(2)存在性问题,往往从假定出发,现设N点位置,这提示要利用空间向量设点的坐标,空间向量解决线面垂直问题的关键在于表示出平面的法向量,也可利用线面垂直的性质,即垂直平面中两条相交直线,由
,(2)存在性问题,往往从假定出发,现设N点位置,这提示要利用空间向量设点的坐标,空间向量解决线面垂直问题的关键在于表示出平面的法向量,也可利用线面垂直的性质,即垂直平面中两条相交直线,由 及
及 解得
解得 ,是
,是 的中点(3)求线面角,关键在于作出平面的垂线,此时可利用(2)的结论,即MN为平面
的中点(3)求线面角,关键在于作出平面的垂线,此时可利用(2)的结论,即MN为平面 的垂线;另外也可继续利用空间向量求线面角,即直线
的垂线;另外也可继续利用空间向量求线面角,即直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 余弦值的绝对值.
余弦值的绝对值.
试题解析:解(1)
 是
是 的中点,取PD的中点
的中点,取PD的中点 ,则
,则

 ,又
,又


 四边形
四边形 为平行四边形
为平行四边形
 ∥
∥ ,
, 平面
平面 ,
, 平面
平面

 ∥平面
∥平面 ..(4分)
..(4分)
(2)以 为原点,以
为原点,以 、
、 、
、 所在直线为
所在直线为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系,如图,则
轴建立空间直角坐标系,如图,则 ,
, ,
, ,
, ,
, ,
,
在平面 内设
内设 ,
, ,
, ,
, 由
由




由







 是
是 的中点,此时
的中点,此时 平面
平面

练习册系列答案
相关题目
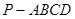 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面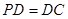 ,
,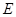 是
是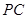 的中点,作
的中点,作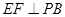 交
交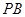 于点
于点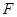 .
.
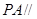 平面
平面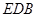 ;
;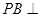 平面
平面 .
. AB,E是SA的中点.
AB,E是SA的中点.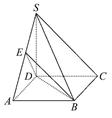
 AD,E为CD上一点,且CE=3DE.
AD,E为CD上一点,且CE=3DE.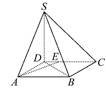
 中,
中,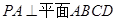 ,底面
,底面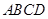 为梯形,
为梯形,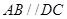 ,
,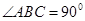 ,且
,且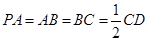 ,
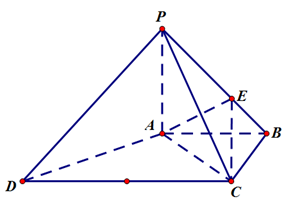
,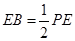 .
.
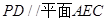 ;
;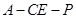 的余弦值.
的余弦值.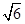 ,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=
,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD= .
.
 ,中,
,中,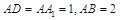 ,点
,点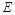 在棱AB上移动.
在棱AB上移动.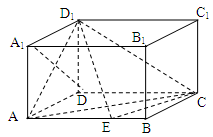
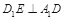 ;
; 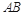 的中点时,求点
的中点时,求点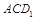 的距离;
的距离; 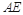 等于何值时,二面角
等于何值时,二面角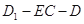 的大小为
的大小为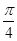 .
.