题目内容
已知函数 .
.
(1)将函数化成 的形式,并写出最小正周期;
的形式,并写出最小正周期;
(2)用“五点法”作函数的图象,并写出该函数在[0,π]上的单调递增区间.
解:y=sin4x+2  sinxcosx-cos4x
sinxcosx-cos4x
=(sin2x+cos2x)(sin2x-cos2x)+ sin2x
sin2x
= sin2x-cos2x
sin2x-cos2x
=2sin(2x- ).
).
(1)该函数的最小正周期是π;
(2)列表:
描点作图:

单调递增区间是
分析:先分解因式,然后利用二倍角的余弦公式以及两角差的余弦,化为一个角的一个三角函数的形式, (1)求出周期;
(1)求出周期;
(2)通过列表描点,用“五点法”作函数的图象,求出函数[0,π]的单调增区间.
点评:本题考查三角函数的周期性及其求法,同角三角函数间的基本关系,二倍角的正弦,二倍角的余弦,正弦函数的单调性,三角函数的最值,把三角函数式化简为y=Asin(ωx+φ)+k(ω>0)是解决周期、最值、单调区间问题的常用方法.
 sinxcosx-cos4x
sinxcosx-cos4x=(sin2x+cos2x)(sin2x-cos2x)+
 sin2x
sin2x=
 sin2x-cos2x
sin2x-cos2x=2sin(2x-
 ).
).(1)该函数的最小正周期是π;
(2)列表:
2x- | 0 |  | π |  | 2π |
| x |  |  |  |  | 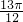 |
2sin(2x- ) ) | 0 | 2 | 0 | -2 | 0 |

单调递增区间是

分析:先分解因式,然后利用二倍角的余弦公式以及两角差的余弦,化为一个角的一个三角函数的形式,
 (1)求出周期;
(1)求出周期;(2)通过列表描点,用“五点法”作函数的图象,求出函数[0,π]的单调增区间.
点评:本题考查三角函数的周期性及其求法,同角三角函数间的基本关系,二倍角的正弦,二倍角的余弦,正弦函数的单调性,三角函数的最值,把三角函数式化简为y=Asin(ωx+φ)+k(ω>0)是解决周期、最值、单调区间问题的常用方法.

练习册系列答案
相关题目