题目内容
以下命题:
①若|
-
|=|
|-|
|,则
∥
;
②
=(-1,1)在
=(3,4)方向上的投影为
;
③若△ABC中,a=5,b=8,c=7,
-
=20;
④若非向量
、
满足|
-
|=|
|,则|2
|>|
+2
|.
其中所有真命题的标号是
①若|
| a |
| b |
| a |
| b |
| a |
| b |
②
| a |
| b |
| 1 |
| 5 |
③若△ABC中,a=5,b=8,c=7,
| BC |
| CA |
④若非向量
| a |
| b |
| a |
| b |
| b |
| b |
| a |
| b |
其中所有真命题的标号是
①②
①②
.分析:①已知|
-
|=|
|-|
|,两边平方,可以对其进行判断;
②
=(-1,1)在
=(3,4),求出两个向量的余弦值,
=(-1,1)在
=(3,4)方向上的投影为|
|cos<
,
>;
③△ABC中,a=5,b=8,c=7,
-
是一个向量,不可能是一个值;
④非向量
、
满足|
-
|=|
|,两边平方可得|
|=2|
|cos<
,
>,利用等价的方法进行证明;
| a |
| b |
| a |
| b |
②
| a |
| b |
| a |
| b |
| b |
| a |
| b |
③△ABC中,a=5,b=8,c=7,
| BC |
| CA |
④非向量
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
解答:解:①∵|
-
|=|
|-|
|,两边平方可得|
|2+|
|2-2
•
=|
|2+|
|2-2|
||
|,
可得
•
=|
||
|,可得cos<
,
>=0,可得
,
平行,可得
∥
,故①正确;
②因为
=(-1,1),
=(3,4)可得cos<
,
>=
=
=
,
∴
=(-1,1)在
=(3,4)方向上的投影为|
|cos<
,
>=
×
=
,故②正确;
③△ABC中,a=5,b=8,c=7,
-
,两个向量相减结果应该是一个向量,不可能为一个数,
故③错误;
④非向量
、
满足|
-
|=|
|,|
|2+|
|2-2
•
=|
|2,可得,|
|2=2
•
,
要证明:|2
|>|
+2
|?4|
|2>|
|2+4|
|2+4
•
?|
|2+2|
|2<0,
因为向量
、
是非零的,|
|>0,可得,|
|2+2|
|2>0,故④错误,
综上①②正确;
故答案为:①②;
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
可得
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
②因为
| a |
| b |
| a |
| b |
| ||||
|
|
| -3+4 | ||
|
| ||
| 10 |
∴
| a |
| b |
| a |
| a |
| b |
| 2 |
| ||
| 10 |
| 1 |
| 5 |
③△ABC中,a=5,b=8,c=7,
| BC |
| CA |
故③错误;
④非向量
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
要证明:|2
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
因为向量
| a |
| b |
| a |
| a |
| a |
综上①②正确;
故答案为:①②;
点评:本题考查命题的真假判断与应用,着重考查向量的数量积与向量的夹角与模,考查综合分析与解决问题的能力,属于中档题.

练习册系列答案
相关题目
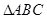 中,若
中,若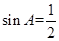 ,则
,则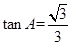 ;
;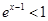 ”是“
”是“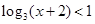 ”的必要不充分条件;
”的必要不充分条件;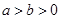 且
且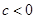 ,则
,则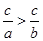 ”的逆命题是真命题.
”的逆命题是真命题.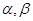 是两个不同的平面,
是两个不同的平面,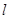 是一条直线,以下命题正确的是
是一条直线,以下命题正确的是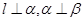 ,则
,则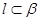 B.若
B.若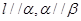 ,则
,则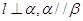 ,则
,则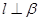 D.若
D.若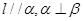 ,则
,则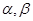 是两个不同的平面,
是两个不同的平面,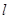 是一条直线,以下命题正确的是
是一条直线,以下命题正确的是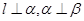 ,则
,则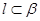 B.若
B.若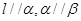 ,则
,则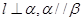 ,则
,则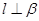 D.若
D.若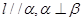 ,则
,则