题目内容
已知两点F1(0,-2),F2(0,2),且点P到这两点的距离和等于6.
(1)求以F1,F2为焦点,且过点P的椭圆方程;
(2)设点P(0,3),F1,F2,P关于直线y=x的对称点分别为P',
,F2′,求以
,F2′为焦点,且过点P′的双曲线方程.
(1)求以F1,F2为焦点,且过点P的椭圆方程;
(2)设点P(0,3),F1,F2,P关于直线y=x的对称点分别为P',
| F | ′ 1 |
| F | ′ 1 |
分析:(1)根据题意设出所求的椭圆的标准方程,然后椭圆定义,得2a,c,再求出b.最后写出椭圆标准方程.
(2)根据三个已知点的坐标,求出关于直线y=x的对称点分别为点,设出所求双曲线标准方程,代入求解即可.
(2)根据三个已知点的坐标,求出关于直线y=x的对称点分别为点,设出所求双曲线标准方程,代入求解即可.
解答:解:(1)设椭圆的方程为
+
=1(a>b>0),
由椭圆定义,得2a=|PF1|+|PF2|=6,c=2,所以,b2=a2-c2=5.
所以,椭圆的方程为
+
=1.…(5分)
(2)因为点P,F1,F2关于直线y=x的对称点分别为P'(3,0),F1′(-2,0),F2′(2,0),
设双曲线的方程为
-
=1(a>0,b>0),
由双曲线定义,得2a=||P'F'1|-|P'F'2||=4,c=
,
所以,b2=c2-a2=10.
所以,双曲线的方程为
-
=1.…(10分)
| y2 |
| a2 |
| x2 |
| b2 |
由椭圆定义,得2a=|PF1|+|PF2|=6,c=2,所以,b2=a2-c2=5.
所以,椭圆的方程为
| y2 |
| 9 |
| x2 |
| 5 |
(2)因为点P,F1,F2关于直线y=x的对称点分别为P'(3,0),F1′(-2,0),F2′(2,0),
设双曲线的方程为
| x2 |
| a2 |
| y2 |
| b2 |
由双曲线定义,得2a=||P'F'1|-|P'F'2||=4,c=
| 14 |
所以,b2=c2-a2=10.
所以,双曲线的方程为
| x2 |
| 4 |
| y2 |
| 10 |
点评:本小题主要考查椭圆与双曲线的基本概念、标准方程、几何性质等基础知识和基本运算能力.属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
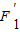 ,
,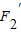 ,求以
,求以 ,
, 为焦点,且过点P′的双曲线方程.
为焦点,且过点P′的双曲线方程.