Question

设函数f（x）=|x²-4x-5|，x∈R．
（1）试求出函数f（x）=|x²-4x-5|的零点
（2）在区间[-2，6]上画出函数f（x）的图象；
（3）写出该函数在R上的单调区间．

Answer 1

解：（1）令f（x）=|x²-4x-5|=0
即x²-4x-5=0
解得x=-1，或x=5
故函数f（x）=|x²-4x-5|的零点为-1，5
（2）函数f（x）=|x²-4x-5|=|（x-2）²-9|，
列表如下：

故函数f（x）=|x²-4x-5|在区间[-2，6]上的图象为：

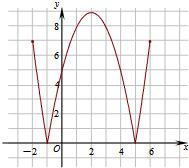
（3）由（2）中图象可得：
函数在（-∞，-1]上单调递减；
函数在[-1，2]上单调递增；
函数在[2，5]上单调递减；
函数在[5，+∞）上单调递增．
分析：（1）根据函数零点的定义，我们可以将求函数f（x）=|x²-4x-5|的零点，转化为求方程|x²-4x-5|=0的根，根据绝对值的定义脱掉绝对值符号，易得答案．
（2）利用描点法我们易画出函数在区间[-2，6]上的图象．
（3）根据（2）的图象，我们将易分析出函数的性质，进而求出该函数在R上的单调区间．
点评：本题考查的知识点是函数零点的判定定理，二次函数的性质，其中画出函数的图象，交借助图象分析函数的性质，是数形结合思想在解答函数问题时的体现，一定要熟练掌握．