题目内容
已知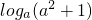 <0
<0
(1)比较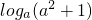 与loga2a的大小.
与loga2a的大小.
(2)解关于x的不等式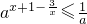 .
.
解:(1)∵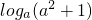 <0,∴0<a<1,故函数y=logax是定义域内的减函数.
<0,∴0<a<1,故函数y=logax是定义域内的减函数.
由于a2+1>2a,∴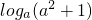 <loga2a.
<loga2a.
(2)由题中条件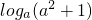 <0,可得0<a<1,
<0,可得0<a<1,
由关于x的不等式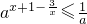 可得 x+1-
可得 x+1- ≥-1,即
≥-1,即  ,
,
用穿根法求得-3≤x<0,或 x≥1,
故不等式的解集为 {x|-3≤x<0,或x≥1}.
分析:(1)由条件可得0<a<1,故函数y=logax是定义域内的减函数,再由a2+1>2a,可得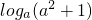 与loga2a 的大小关系.
与loga2a 的大小关系.
(2)由关于x的不等式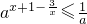 可得 x+1-
可得 x+1- ≥-1,即
≥-1,即 ,解此分式不等式,求得结果.
,解此分式不等式,求得结果.
点评:本题主要考查指数不等式对数不等式的解法,判断0<a<1,是解题的关键,属于中档题.
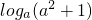 <0,∴0<a<1,故函数y=logax是定义域内的减函数.
<0,∴0<a<1,故函数y=logax是定义域内的减函数.由于a2+1>2a,∴
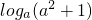 <loga2a.
<loga2a.(2)由题中条件
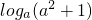 <0,可得0<a<1,
<0,可得0<a<1,由关于x的不等式
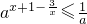 可得 x+1-
可得 x+1- ≥-1,即
≥-1,即  ,
,用穿根法求得-3≤x<0,或 x≥1,
故不等式的解集为 {x|-3≤x<0,或x≥1}.
分析:(1)由条件可得0<a<1,故函数y=logax是定义域内的减函数,再由a2+1>2a,可得
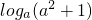 与loga2a 的大小关系.
与loga2a 的大小关系.(2)由关于x的不等式
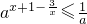 可得 x+1-
可得 x+1- ≥-1,即
≥-1,即 ,解此分式不等式,求得结果.
,解此分式不等式,求得结果.点评:本题主要考查指数不等式对数不等式的解法,判断0<a<1,是解题的关键,属于中档题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目