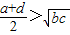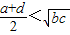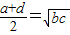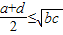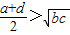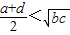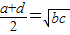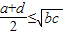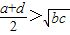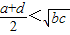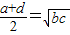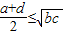题目内容

四个不相等的正数a，b，c，d成等差数列，则（　　）
A．
a+d
2
＞
bc
B．
a+d
2
＜
bc
C．
a+d
2
=
bc
D．
a+d
2
≤
bc
∵四个不相等的正数a、b、c、d成等差数列，
∴b+c=a+d，
又由基本不等式可得：b+c＞2
bc
，
则a+d＞2
bc
，即
a+d
2
＞
bc
．
故选A．
练习册系列答案
相关题目
四个不相等的正数a，b，c，d成等差数列，则（　　）
四个不相等的正数a、b、c、d成等差数列，则下列关系式一定成立的是（　　）
A、
a+d
2
＜
bc
B、
a+d
2
＞
bc
C、
a+d
2
=
bc
D、
a+c
2
＞
bd
四个不相等的正数a，b，c，d成等差数列，则（ ）
A．
B．
C．
D．
四个不相等的正数a，b，c，d成等差数列，则（ ）
A．
B．
C．
D．
四个不相等的正数a，b，c，d成等差数列，则（ ）
A．
B．
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网