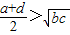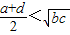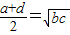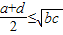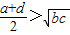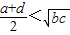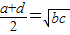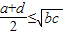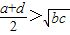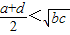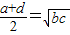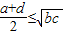题目内容
四个不相等的正数a，b，c，d成等差数列，则（ ）
分析：根据等差数列的定义和性质可得b+c=a+d，再由基本不等式可得b+c＞2
，等量代换变形可得到答案．
| bc |
解答：解：∵四个不相等的正数a、b、c、d成等差数列，
∴b+c=a+d，
又由基本不等式可得：b+c＞2
，
则a+d＞2
，即
＞
．
故选A．
∴b+c=a+d，
又由基本不等式可得：b+c＞2
| bc |
则a+d＞2
| bc |
| a+d |
| 2 |
| bc |
故选A．
点评：本题考查等差数列的定义和性质，基本不等式的应用，利用等差数列的性质得到b+c=a+d是解题的关键．
练习册系列答案
相关题目
四个不相等的正数a、b、c、d成等差数列，则下列关系式一定成立的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
