题目内容
函数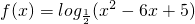 在(a,+∞)上是减函数,则实数a的最小值是________.
在(a,+∞)上是减函数,则实数a的最小值是________.
5
分析:先求出函数的定义域,根据复合函数的单调性可得函数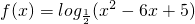 在(5,+∞)上是减函数,得
在(5,+∞)上是减函数,得
a≥5,由此求得实数a的最小值.
解答:由于函数y=x2-6x+5>0可得 x<1,或 x>5.
由复合函数的单调性可得函数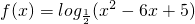 在(5,+∞)上是减函数,
在(5,+∞)上是减函数,
在(-∞,1)上是增函数.
再由函数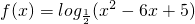 在(a,+∞)上是减函数,可得a≥5,
在(a,+∞)上是减函数,可得a≥5,
故实数a的最小值是5,
故答案为 5.
点评:本题主要考查对数函数的单调性和特殊点,对数函数的定义域,复合函数的单调性规律,二次函数的性质,属于基础题.
分析:先求出函数的定义域,根据复合函数的单调性可得函数
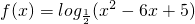 在(5,+∞)上是减函数,得
在(5,+∞)上是减函数,得a≥5,由此求得实数a的最小值.
解答:由于函数y=x2-6x+5>0可得 x<1,或 x>5.
由复合函数的单调性可得函数
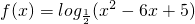 在(5,+∞)上是减函数,
在(5,+∞)上是减函数,在(-∞,1)上是增函数.
再由函数
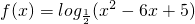 在(a,+∞)上是减函数,可得a≥5,
在(a,+∞)上是减函数,可得a≥5,故实数a的最小值是5,
故答案为 5.
点评:本题主要考查对数函数的单调性和特殊点,对数函数的定义域,复合函数的单调性规律,二次函数的性质,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
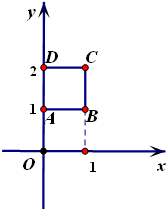 已知f(x)=2|x-1|,该函数在区间[a,b]上的值域为[1,2],记满足该条件的实数a、b所形成的实数对为点P(a,b),则由点P构成的点集组成的图形为( )
已知f(x)=2|x-1|,该函数在区间[a,b]上的值域为[1,2],记满足该条件的实数a、b所形成的实数对为点P(a,b),则由点P构成的点集组成的图形为( )