题目内容
若向量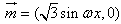 ,
,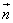 =(cosωx,-sinωx)(ω>0),在函数f(x)=
=(cosωx,-sinωx)(ω>0),在函数f(x)= +t的图象中,对称中心到对称轴的最小距离为
+t的图象中,对称中心到对称轴的最小距离为 ,且当x∈
,且当x∈ 时,f(x)的最大值为1,
时,f(x)的最大值为1,
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的单调递增区间。
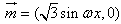 ,
,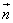 =(cosωx,-sinωx)(ω>0),在函数f(x)=
=(cosωx,-sinωx)(ω>0),在函数f(x)= +t的图象中,对称中心到对称轴的最小距离为
+t的图象中,对称中心到对称轴的最小距离为 ,且当x∈
,且当x∈ 时,f(x)的最大值为1,
时,f(x)的最大值为1, (Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的单调递增区间。
解:(Ⅰ)由题意得
 +t
+t

 ,
,
∵对称中心到对称轴的最小距离为 ,
,
∴f(x)的最小正周期为T=π,
∴ ,∴
,∴ ,
,
∴ ,
,
当 ,
,
∴ 时,f(x)取得最大值3+t,
时,f(x)取得最大值3+t,
 ,
,
∴3+t=1,∴t=-2,
∴ 。
。
(Ⅱ) ,
,
 ,
,
∴函数f(x)的单调递增区间为 。
。
 +t
+t
 ,
,∵对称中心到对称轴的最小距离为
 ,
,∴f(x)的最小正周期为T=π,
∴
 ,∴
,∴ ,
,∴
 ,
,当
 ,
,∴
 时,f(x)取得最大值3+t,
时,f(x)取得最大值3+t, ,
,∴3+t=1,∴t=-2,
∴
 。
。(Ⅱ)
 ,
, ,
,∴函数f(x)的单调递增区间为
 。
。
练习册系列答案
相关题目
 ,
, ,则cos<
,则cos< >= .
>= .