题目内容
【题目】如图，在梯形ABCD中，AB∥CD，CD＝2，△ABC是边长为3的等边三角形．
（1）求AD；
（2）求sin∠DAB．
【答案】（1）
；（2）
.
【解析】
（1）利用平行线的性质以及题的条件，得到
，
，利用余弦定理求得
的长度；
（2）法1：在
中，应用正弦定理求得
的值，利用同旁内角互补以及诱导公式求得sin∠DAB的值；法2：利用余弦定理求得
的值，利用同角三角函数关系求得
，利用正弦和角公式求得sin∠DAB的值.
（1）在梯形ABCD中，因为
，
是边长为3的等边三角形，
所以，．
在中，由余弦定理，得
，
所以．
（2）法1：在中，由正弦定理，得
，
结合（1）知，
．
因为，所以
．
从而
．
法2：在中，由余弦定理，得
结合（1）知，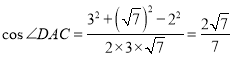
．
从而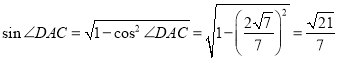
．
所以
．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某制造商
月生产了一批乒乓球，随机抽样
个进行检查，测得每个球的直径(单位：mm)，将数据分组如下表
分组 | 频数 | 频率 |
| 10 | |
| 20 | |
| 50 | |
| 20 | |
合计 | 100 |
(1)请在上表中补充完成频率分布表(结果保留两位小数)，并在上图中画出频率分布直方图；
(2)统计方法中，同一组数据常用该组区间的中点值(例如区间
的中点值是
)作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
