题目内容
角α的顶点在坐标原点O,始边在y轴的正半轴上,终边在第三象限过点P,且 ;角β的顶点在坐标原点O,始边在x轴的正半轴上,终边在第二象限经过点Q,且tanβ=-2,则cos∠POQ的值为
;角β的顶点在坐标原点O,始边在x轴的正半轴上,终边在第二象限经过点Q,且tanβ=-2,则cos∠POQ的值为
- A.

- B.
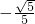
- C.

- D.

B
分析:由题意可得在[0,2π]上,α、β都为钝角,且∠POQ=α+ -β,0<α-β<
-β,0<α-β< .利用两角差的正切公式求得tan(α-β),可得sin(α-β)的值,再由cos∠POQ=-sin(α-β) 运算求得结果.
.利用两角差的正切公式求得tan(α-β),可得sin(α-β)的值,再由cos∠POQ=-sin(α-β) 运算求得结果.
解答:由题意可得在[0,2π]上,α、β都为钝角,α>β,且∠POQ=α+ -β,∴0<α-β<
-β,∴0<α-β< .
.
∵tan(α-β)= =
= =
= ,
,
再由 cos(α-β)2+sin(α-β)2=1,求得cos(α-β)= ,sin(α-β)=
,sin(α-β)= ,
,
故 cos∠POQ=cos(α+ -β )=-sin(α-β)=-
-β )=-sin(α-β)=- ,
,
故选B.
点评:本题考查两角和与差的正切函数,同角三角函数的基本关系,突出三角函数的综合应用,属于中档题.
分析:由题意可得在[0,2π]上,α、β都为钝角,且∠POQ=α+
 -β,0<α-β<
-β,0<α-β< .利用两角差的正切公式求得tan(α-β),可得sin(α-β)的值,再由cos∠POQ=-sin(α-β) 运算求得结果.
.利用两角差的正切公式求得tan(α-β),可得sin(α-β)的值,再由cos∠POQ=-sin(α-β) 运算求得结果.解答:由题意可得在[0,2π]上,α、β都为钝角,α>β,且∠POQ=α+
 -β,∴0<α-β<
-β,∴0<α-β< .
.∵tan(α-β)=
 =
= =
= ,
,再由 cos(α-β)2+sin(α-β)2=1,求得cos(α-β)=
 ,sin(α-β)=
,sin(α-β)= ,
,故 cos∠POQ=cos(α+
 -β )=-sin(α-β)=-
-β )=-sin(α-β)=- ,
,故选B.
点评:本题考查两角和与差的正切函数,同角三角函数的基本关系,突出三角函数的综合应用,属于中档题.

练习册系列答案
相关题目
 cos2x+sinxcosx-
cos2x+sinxcosx- ,x∈R.
,x∈R.