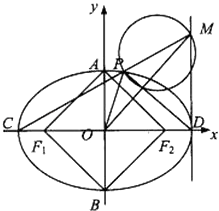
题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 和抛物线
和抛物线![]() 交于
交于![]() 两点,且直线
两点,且直线![]() 恰好通过椭圆
恰好通过椭圆![]() 的右焦点
的右焦点![]() ,
,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过![]() 的直线
的直线![]() 和椭圆
和椭圆![]() 交于
交于![]() 两点,交抛物线于
两点,交抛物线于![]() 两点,
两点, ![]() 是抛物线的焦点,是否存在直线
是抛物线的焦点,是否存在直线![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
【答案】(1) ![]() ;(2) 存在直线
;(2) 存在直线![]() :
: ![]() 或者
或者![]() 满足条件.
满足条件.
【解析】【试题分析】(1)先借助题设条件求出交点坐标![]() ,再代入椭圆方程与离心率联立方程组求解;(2)先建立直线
,再代入椭圆方程与离心率联立方程组求解;(2)先建立直线![]() 为
为![]() ,再与椭圆方程联立方程组
,再与椭圆方程联立方程组 ,借助题设条件求得
,借助题设条件求得![]() ,运用弦长公式求出弦长建立方程
,运用弦长公式求出弦长建立方程 ,进而求出直线的斜率
,进而求出直线的斜率![]() :
:
解:(1)由![]() 知,可设
知,可设![]() ,其中
,其中![]()
由已知![]() ,代入椭圆中得:
,代入椭圆中得: ![]() 即
即![]() ,解得
,解得![]()
从而![]() ,故椭圆方程为
,故椭圆方程为![]()
(2)易知,直线![]() 的斜率存在。设直线
的斜率存在。设直线![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 。由条件知
。由条件知![]() 。
。 ,故
,故![]() 。
。
由 ,
,
![]()
![]()
![]()
![]()

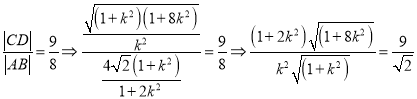
![]()
![]() 。存在直线
。存在直线![]() :
: ![]() 或者
或者![]() 满足条件。
满足条件。

练习册系列答案
相关题目
【题目】甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5次预赛成绩记录如下:
甲 | 82 | 82 | 79 | 95 | 87 |
乙 | 95 | 75 | 80 | 90 | 85 |
(1)请用茎叶图表示这两组数据;
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)现要从中选派一人参加9月份的全国数学联赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由.