题目内容
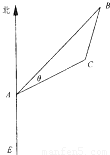
位于A处的雷达观测站,发现其北偏东45°,与A相距20 海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(0°<θ<45°)的C处,
海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(0°<θ<45°)的C处, .在离观测站A的正南方某处E,cos∠EAC=-
.在离观测站A的正南方某处E,cos∠EAC=-
(1)求cosθ;
(2)求该船的行驶速度v(海里/小时).

【答案】分析:(1)利用同角三角函数的基本关系求得sin∠EAC的值,根据 ,利用两角差的余弦公式求得结果.
,利用两角差的余弦公式求得结果.
(2)利用余弦定理求得BC的值,而且BC这段距离该船行驶了20分钟,由此求得该船的行驶速度.
解答:解:(1)∵ ,∴
,∴ .(2分)
.(2分)
∴ =
= .(6分)
.(6分)
(2)利用余弦定理求得 BC2=AB2+AC2-2AB•AC•cosθ=125,∴ .(10分)
.(10分)
又该船以匀速直线行驶了20分钟的路程为 海里,
海里,
该船的行驶速度 (海里/小时).(14分)
(海里/小时).(14分)
点评:本题主要考查利用余弦定理求三角形的边长,同角三角函数的基本关系,两角差的余弦公式的应用,属于中档题.
 ,利用两角差的余弦公式求得结果.
,利用两角差的余弦公式求得结果.(2)利用余弦定理求得BC的值,而且BC这段距离该船行驶了20分钟,由此求得该船的行驶速度.
解答:解:(1)∵
 ,∴
,∴ .(2分)
.(2分)∴
 =
= .(6分)
.(6分)(2)利用余弦定理求得 BC2=AB2+AC2-2AB•AC•cosθ=125,∴
 .(10分)
.(10分)又该船以匀速直线行驶了20分钟的路程为
 海里,
海里,该船的行驶速度
 (海里/小时).(14分)
(海里/小时).(14分)点评:本题主要考查利用余弦定理求三角形的边长,同角三角函数的基本关系,两角差的余弦公式的应用,属于中档题.

练习册系列答案
相关题目
 (2013•奉贤区二模)位于A处的雷达观测站,发现其北偏东45°,与A相距20
(2013•奉贤区二模)位于A处的雷达观测站,发现其北偏东45°,与A相距20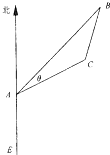 如图,有一位于A处的雷达观测站发现其北偏东45°,与A相距
如图,有一位于A处的雷达观测站发现其北偏东45°,与A相距 相距20
相距20 海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东
海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东
 的C处,
的C处, .在离观测站A的正南方某处E,
.在离观测站A的正南方某处E,

 ; (2)求该船的行驶速度v(海里/小时);
; (2)求该船的行驶速度v(海里/小时);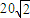 海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中
海里的B处有一货船正以匀速直线行驶,20分钟后又测得该船只位于观测站A北偏东45°+θ(其中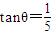 ,0°<θ<45°)且与观测站A相距
,0°<θ<45°)且与观测站A相距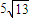 海里的C处.
海里的C处.