题目内容
函数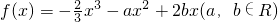 在区间[-1,2]上单调递增,则
在区间[-1,2]上单调递增,则 的取值范围是
的取值范围是
- A.(-∞,-1)∪(2,+∞)
- B.(2,+∞)
- C.(-∞,-1)
- D.(-1,2)
A
分析:根据导数与函数单调性的关系可得f′(x)=-2x2-2ax+2b≥0在区间[-1,2]上恒成立,再结合二次函数的图象得到两个不等式,进而转化为线性规划问题,根据 的几何意义是表示两点的连线的斜率,进而求解出答案即可.
的几何意义是表示两点的连线的斜率,进而求解出答案即可.
解答: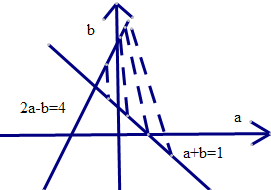 解:因为函数
解:因为函数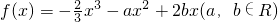 在区间[-1,2]上单调递增,
在区间[-1,2]上单调递增,
所以f′(x)=-2x2-2ax+2b≥0在区间[-1,2]上恒成立,
即x2+ax-b≤0在区间[-1,2]上恒成立,
所以a+b≥1,2a-b+4≥0,
所以可得平面区域为:
则 =
=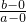 表示点(0,0)与点(a,b)连线的斜率,
表示点(0,0)与点(a,b)连线的斜率,
所以 的范围为(-∞,-1)∪(2,+∞).
的范围为(-∞,-1)∪(2,+∞).
故选A.
点评:解决此类问题的关键是熟练掌握导数与函数单调性的关系以及不等式的恒成立问题,而对于线性规划问题也是高考常考问题.
分析:根据导数与函数单调性的关系可得f′(x)=-2x2-2ax+2b≥0在区间[-1,2]上恒成立,再结合二次函数的图象得到两个不等式,进而转化为线性规划问题,根据
 的几何意义是表示两点的连线的斜率,进而求解出答案即可.
的几何意义是表示两点的连线的斜率,进而求解出答案即可.解答:
 解:因为函数
解:因为函数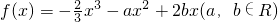 在区间[-1,2]上单调递增,
在区间[-1,2]上单调递增,所以f′(x)=-2x2-2ax+2b≥0在区间[-1,2]上恒成立,
即x2+ax-b≤0在区间[-1,2]上恒成立,
所以a+b≥1,2a-b+4≥0,
所以可得平面区域为:
则
 =
=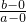 表示点(0,0)与点(a,b)连线的斜率,
表示点(0,0)与点(a,b)连线的斜率,所以
 的范围为(-∞,-1)∪(2,+∞).
的范围为(-∞,-1)∪(2,+∞).故选A.
点评:解决此类问题的关键是熟练掌握导数与函数单调性的关系以及不等式的恒成立问题,而对于线性规划问题也是高考常考问题.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 ,当
,当 >0时,若函数
>0时,若函数 在区间[-1、2]上是减函数,求
在区间[-1、2]上是减函数,求 在区间[1,2]上是增函数,则实数a的取值范围是 .
在区间[1,2]上是增函数,则实数a的取值范围是 .