题目内容
1.用“五点作图法”画出y=$\sqrt{2}$sin(2x+$\frac{π}{4}$)在[0,π]上图象.分析 当x∈[0,π]时,2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{9π}{4}$],用五点作图法在给出的坐标系中画出y=f(x)在[0,π]上的图象即可.
解答 解:当x∈[0,π]时,2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{9π}{4}$],
列表如下:
| 2x+$\frac{π}{4}$ | $\frac{π}{4}$ | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π | $\frac{9π}{4}$ |
| x | 0 | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ | π |
| y | 1 | $\sqrt{2}$ | 0 | -$\sqrt{2}$ | 0 | 1 |
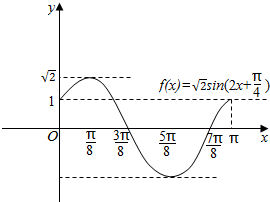
点评 本题考查五点法作函数y=Asin(ωx+φ)的图象,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
11.在平面直角坐标系中,点O(0,0),P(3,$\sqrt{3}$),将向量$\overrightarrow{OP}$饶点O按逆时针方向旋转$\frac{π}{2}$后得向量$\overrightarrow{OQ}$,则点Q的坐标是( )
| A. | (-3,$\sqrt{3}$) | B. | (-$\sqrt{6}$,$\sqrt{6}$) | C. | (-$\sqrt{3}$,3) | D. | (-3,3) |
15.已知x,y满足$\left\{\begin{array}{l}x+2y-4≤0\\ x-y-1≤0\\ x≥1\end{array}\right.$若ax+y≥1恒成立,则实数a的取值范围是( )
| A. | $a≥-\frac{1}{2}$ | B. | $a≥\frac{1}{2}$ | C. | a≥1 | D. | $-\frac{1}{2}≤a≤1$ |