题目内容
已知关于x的一元二次函数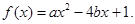
(1)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为 和
和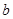 ,
,
求函数 在区间[
在区间[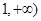 上是增函数的概率;
上是增函数的概率;
(2)设点( ,
,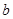 )是区域
)是区域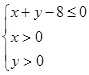 内的随机点,求函数
内的随机点,求函数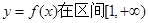 上是增函数的概率.
上是增函数的概率.
(1)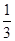 ;(2)
;(2)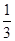
解析试题分析:(1)考查古典概型,满足条件的是5个,总的基本事件个数是15个,求两者的比即可;(2)考查几何概型,求出满足条件的区域面积比上总的区域面积即可.
试题解析:(1)∵函数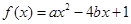 的图象的对称轴为
的图象的对称轴为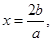
要使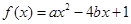 在区间
在区间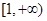 上为增函数,当且仅当
上为增函数,当且仅当 >0且
>0且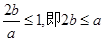 ,
,
若 =1则
=1则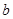 =-1;若
=-1;若 =2则
=2则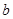 =-1,1;若
=-1,1;若 =3则
=3则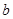 =-1,1;
=-1,1;
∴事件包含基本事件的个数是1+2+2=5,
∴所求事件的概率为 . 6分
. 6分
(2)由(1)知当且仅当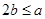 且
且 >0时,函数
>0时,函数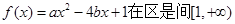 上为增函数,
上为增函数,
依条件可知试验的全部结果所构成的区域为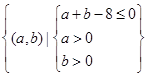 ,构成所求事件的区域为三角形部分.
,构成所求事件的区域为三角形部分.
由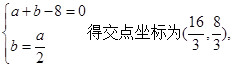
∴所求事件的概率为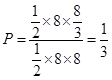 . 12分
. 12分
考点:(1)古典概型;(2)几何概型.

练习册系列答案
相关题目
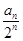 ,求Tn.
,求Tn.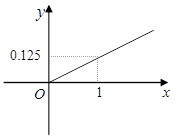
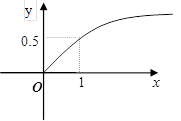

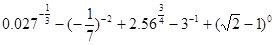
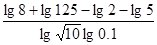
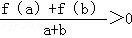 .
.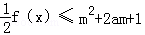 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围. 万件与年广告费用
万件与年广告费用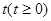 万元满足关系式:
万元满足关系式: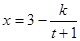 (
( 为常数).若不做广告,则产品的年销售量恰好为1万件.已知2014年生产该产品时,该厂需要先固定投入8万元,并且预计生产每1万件该产品时,需再投入4万元,每件产品的销售价格定为每件产品所需的年平均成本的1.5倍(每件产品的成本包括固定投入和生产再投入两部分,不包括广告促销费用).
为常数).若不做广告,则产品的年销售量恰好为1万件.已知2014年生产该产品时,该厂需要先固定投入8万元,并且预计生产每1万件该产品时,需再投入4万元,每件产品的销售价格定为每件产品所需的年平均成本的1.5倍(每件产品的成本包括固定投入和生产再投入两部分,不包括广告促销费用).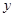 (万元)表示为年广告促销费用
(万元)表示为年广告促销费用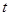 (万元)的函数;
(万元)的函数;