题目内容
设函数g（x）=1-2x，f（g（x））=
（x≠0），则f（
）=（ ）
| 1-x |
| x |
| 1 |
| 2 |
分析：由g（x）=
得x=
，则f（
）=f[g（
）]，代入已知表达式可得答案．
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解答：解：令g（x）=1-2x=
，解得x=
，
所以f（
）=f[g（
）]=
=3，
故选B．
| 1 |
| 2 |
| 1 |
| 4 |
所以f（
| 1 |
| 2 |
| 1 |
| 4 |
1-
| ||
|
故选B．
点评：本题考查函数的性质及函数求值，属基础题．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
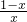（x≠0），则f（
）=
（x≠0），则f（
）=（ ）