题目内容
已知定点C(-1,0)及椭圆x2+3y2=5,过点C的动直线与椭圆相交于A,B两点.(Ⅰ)若线段AB中点的横坐标是
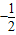 ,求直线AB的方程;
,求直线AB的方程;(Ⅱ)设点M的坐标为
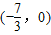 ,求
,求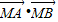 的值.
的值.
【答案】分析:(1)将直线的点斜式方程(其中斜率为参数)代入椭圆方程,并设出交点A,B的坐标,消去Y后,可得一个关于X的一元二次方程,然后根据韦达定理(一元二次方程根与系数关系)易得A、B两点中点的坐标表达式,再由AB中点的横坐标是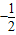 ,构造方程,即可求出直线的斜率,进而得到直线的方程.
,构造方程,即可求出直线的斜率,进而得到直线的方程.
(2)由M点的坐标,我们易给出两个向量的坐标,然后代入平面向量数量集公式,结合韦达定理(一元二次方程根与系数关系),不难不求出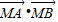 的值.
的值.
解答:解:(Ⅰ)依题意,直线AB的斜率存在,设直线AB的方程为y=k(x+1),
将y=k(x+1)代入x2+3y2=5,消去y整理得(3k2+1)x2+6k2x+3k2-5=0.
设A(x1,y1),B(x2,y2),则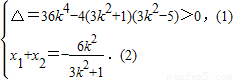
由线段AB中点的横坐标是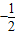 ,得
,得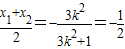 ,
,
解得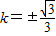 ,适合(1).
,适合(1).
所以直线AB的方程为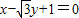 ,或
,或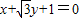 .
.
(Ⅱ)①当直线AB与x轴不垂直时,由(Ⅰ)知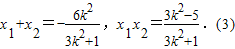
所以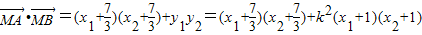 =
=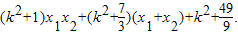
将(3)代入,整理得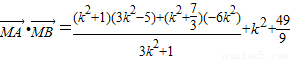 =
=
②当直线AB与x轴垂直时,此时点A,B的坐标分别为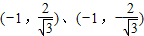 ,
,
此时亦有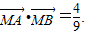
综上,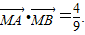
点评:与直线和圆锥曲线的位置关系有关的参数范围问题,常采用解方程组的思想方法,转化为判别式进行;与向量数量积有关的问题,常常利用韦达定理,以整体代入的方法求解,这样可以避免求交点,使运算过程得到简化.
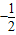 ,构造方程,即可求出直线的斜率,进而得到直线的方程.
,构造方程,即可求出直线的斜率,进而得到直线的方程.(2)由M点的坐标,我们易给出两个向量的坐标,然后代入平面向量数量集公式,结合韦达定理(一元二次方程根与系数关系),不难不求出
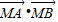 的值.
的值.解答:解:(Ⅰ)依题意,直线AB的斜率存在,设直线AB的方程为y=k(x+1),
将y=k(x+1)代入x2+3y2=5,消去y整理得(3k2+1)x2+6k2x+3k2-5=0.
设A(x1,y1),B(x2,y2),则
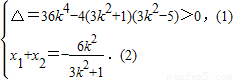
由线段AB中点的横坐标是
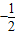 ,得
,得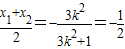 ,
,解得
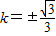 ,适合(1).
,适合(1).所以直线AB的方程为
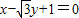 ,或
,或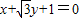 .
.(Ⅱ)①当直线AB与x轴不垂直时,由(Ⅰ)知
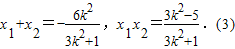
所以
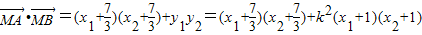 =
=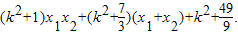
将(3)代入,整理得
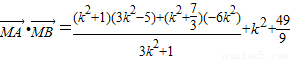 =
=
②当直线AB与x轴垂直时,此时点A,B的坐标分别为
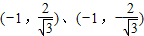 ,
,此时亦有
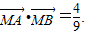
综上,
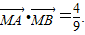
点评:与直线和圆锥曲线的位置关系有关的参数范围问题,常采用解方程组的思想方法,转化为判别式进行;与向量数量积有关的问题,常常利用韦达定理,以整体代入的方法求解,这样可以避免求交点,使运算过程得到简化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目