题目内容
10.已知f(x)是定义在R上周期为4的奇函数,当x∈(0,2]时,f(x)=3x-log3x,则f(2015)=-3.分析 得出f(x+4)=f(x),f(-x)=-f(x),求解即可f(2015)=f(-1+2016)=f(-1)=-f(1)=-3
解答 解:∵f(x)是定义在R上周期为4的奇函数,
∴f(x+4)=f(x),f(-x)=-f(x),
∵当x∈(0,2]时,f(x)=3x+log3x,
∴f(2015)=f(-1+2016)=f(-1)=-f(1)=-3
故答案为:-3.
点评 本题考查了函数的奇偶性,周期性,难度不大,关键是转为给定的区间上的函数值,属于容易题

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
2.将$y=sin(x+\frac{π}{3})$的图象上各点的横坐标缩短到原来的一半,纵坐标不变,再将图象上所有点向左平移$\frac{π}{6}$个单位,则所得函数图象的一条对称轴为( )
| A. | $x=-\frac{π}{12}$ | B. | $x=-\frac{π}{6}$ | C. | $x=\frac{π}{6}$ | D. | $x=\frac{π}{2}$ |
18.已知集合A={x|-2<x<1},B={x|x2-2x≤0},则A∩B=( )
| A. | {x|0<x<1} | B. | {x|0≤x<1} | C. | {x|-1<x≤1} | D. | {x|-2<x≤1} |
5.下列说法中,正确的是( )
| A. | ?α,β∈R,sin(α+β)≠sinα+sinβ | |
| B. | 命题p:?x∈R,x2-x>0,则?p:?x∈R,x2-x<0 | |
| C. | 在△ABC中,“$\overrightarrow{AB}•\overrightarrow{AC}>0$”是“△ABC为锐角三角形”的必要不充分条件 | |
| D. | 已知x∈R,则“x>1”是“x>2”成立的充分不必要条件 |
 和点
和点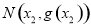 分别是函数
分别是函数 和
和 图象上的点,且
图象上的点,且 ,若直线
,若直线 轴,则
轴,则 两点间的距离的最小值为( )
两点间的距离的最小值为( ) ,设
,设 ,且
,且 ,则
,则 的最小值为( )
的最小值为( ) D.
D.
 的值域是 .
的值域是 . (如图),要测量
(如图),要测量 ,测得
,测得 ,则
,则 .
.