题目内容
已知a>1,则不等式a+
的最小值为
| 2 |
| a-1 |
1+2
.
| 2 |
1+2
.
.| 2 |
分析:由基本不等式可得a+
=a-1+
+1≥1+2
,检验取等号的条件.
| 2 |
| a-1 |
| 2 |
| a-1 |
| 2 |
解答:解:a+
=a-1+
+1≥1+2
,
当且仅当a-1=
,即a=1+
时等号成立.
∴不等式a+
的最小值为1+2
.
故答案为1+2
.
| 2 |
| a-1 |
| 2 |
| a-1 |
| 2 |
当且仅当a-1=
| 2 |
| a-1 |
| 2 |
∴不等式a+
| 2 |
| a-1 |
| 2 |
故答案为1+2
| 2 |
点评:本题考查基本不等式的应用,式子的变形是解题的关键.基本不等式使用的条件:一正、二定、三相等.

练习册系列答案
相关题目
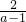 的最小值为________.
的最小值为________.