题目内容
设f(x)是x的三次多项式,已知 =
= =
=
 =1.试求
=1.试求
 的值(a为非零常数).
的值(a为非零常数).
【答案】分析:由题意可知f(x)必含有(x-2a)与(x-4a)的因式,由于f(x)是x的三次多项式,故可设f(x)=A(x-2a)(x-4a)(x-C).由
 =
= A(x-4a)(x-C)=1,得4a2A-2aCA=-1.同理,得8a2A-2aCA=1.从而得到
A(x-4a)(x-C)=1,得4a2A-2aCA=-1.同理,得8a2A-2aCA=1.从而得到
 的值.
的值.
解答:解:由于
 =1,可知f(2a)=0.①
=1,可知f(2a)=0.①
同理f(4a)=0.②
由①②,可知f(x)必含有(x-2a)与(x-4a)的因式,
由于f(x)是x的三次多项式,故可设f(x)=A(x-2a)(x-4a)(x-C).
这里A、C均为待定的常数.
由
 =1,即
=1,即

= A(x-4a)(x-C)=1,
A(x-4a)(x-C)=1,
得A(2a-4a)(2a-C)=1,
即4a2A-2aCA=-1.③
同理,由于
 =1,
=1,
得A(4a-2a)(4a-C)=1,
即8a2A-2aCA=1.④
由③④得C=3a,A= ,
,
因而f(x)= (x-2a)(x-4a)(x-3a).
(x-2a)(x-4a)(x-3a).
∴
 =
=
 (x-2a)(x-4a)
(x-2a)(x-4a)
= •a•(-a)=-
•a•(-a)=- .
.
点评:本题考查数列的极限和性质,解题时要认真审题,仔细解答.

 =
= A(x-4a)(x-C)=1,得4a2A-2aCA=-1.同理,得8a2A-2aCA=1.从而得到
A(x-4a)(x-C)=1,得4a2A-2aCA=-1.同理,得8a2A-2aCA=1.从而得到
 的值.
的值.解答:解:由于

 =1,可知f(2a)=0.①
=1,可知f(2a)=0.①同理f(4a)=0.②
由①②,可知f(x)必含有(x-2a)与(x-4a)的因式,
由于f(x)是x的三次多项式,故可设f(x)=A(x-2a)(x-4a)(x-C).
这里A、C均为待定的常数.
由

 =1,即
=1,即

=
 A(x-4a)(x-C)=1,
A(x-4a)(x-C)=1,得A(2a-4a)(2a-C)=1,
即4a2A-2aCA=-1.③
同理,由于

 =1,
=1,得A(4a-2a)(4a-C)=1,
即8a2A-2aCA=1.④
由③④得C=3a,A=
 ,
,因而f(x)=
 (x-2a)(x-4a)(x-3a).
(x-2a)(x-4a)(x-3a).∴

 =
=
 (x-2a)(x-4a)
(x-2a)(x-4a)=
 •a•(-a)=-
•a•(-a)=- .
.点评:本题考查数列的极限和性质,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
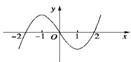 7、设f(x)是一个三次函数,f′(x)为其导函数,如图所示的是y=x•f′(x)的图象的一部分,则f(x)的极大值与极小值分别是( )
7、设f(x)是一个三次函数,f′(x)为其导函数,如图所示的是y=x•f′(x)的图象的一部分,则f(x)的极大值与极小值分别是( ) 设f(x)是一个三次函数,f′(x)为其导函数,如图所示的是y=x•f′(x)的图象的一部分,则f(x)的极大值与极小值分别是( )
设f(x)是一个三次函数,f′(x)为其导函数,如图所示的是y=x•f′(x)的图象的一部分,则f(x)的极大值与极小值分别是( )