题目内容
已知向量 =(-cosx,sinx),
=(-cosx,sinx), ,函数f(x)=
,函数f(x)= .
.
(1)求函数f(x)的解析式;
(2)求函数f(x)的最小正周期、单调增区间;
(3)求函数f(x)在x∈[0,π]时的最大值及相应的x的值.
解:(1)
= =
= ;
;
(2)由(1) ,
,
所以最小正周期 ;
;
 ,解
,解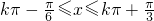 ,
,
所以函数的单调递增区间 .
.
(3)当x∈[0,π]时 ,所
,所 ,
,
当 ,即
,即 时f(x)取最大值,
时f(x)取最大值, .
.
分析:(1)利用向量的坐标运算,结合三角函数中的辅助角公式可以求得f(x)的解析式;
(2)由(1)得到f(x)= ,利用正弦函数的周期公式,可求得其最小正周期,利用正弦函数的单调性可求其单调增区间;
,利用正弦函数的周期公式,可求得其最小正周期,利用正弦函数的单调性可求其单调增区间;
(3)当x∈[0,π],易求2x ,从而可求得f(x)的最大值及相应的x的值.
,从而可求得f(x)的最大值及相应的x的值.
点评:本题考查三角函数的性质,关键是掌握好三角函数特别是正弦函数、余弦函数的单调性,最值,周期及图象等性质,是中档题.

=
 =
= ;
;(2)由(1)
 ,
,所以最小正周期
 ;
; ,解
,解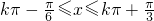 ,
,所以函数的单调递增区间
 .
.(3)当x∈[0,π]时
 ,所
,所 ,
,当
 ,即
,即 时f(x)取最大值,
时f(x)取最大值, .
.分析:(1)利用向量的坐标运算,结合三角函数中的辅助角公式可以求得f(x)的解析式;
(2)由(1)得到f(x)=
 ,利用正弦函数的周期公式,可求得其最小正周期,利用正弦函数的单调性可求其单调增区间;
,利用正弦函数的周期公式,可求得其最小正周期,利用正弦函数的单调性可求其单调增区间;(3)当x∈[0,π],易求2x
 ,从而可求得f(x)的最大值及相应的x的值.
,从而可求得f(x)的最大值及相应的x的值.点评:本题考查三角函数的性质,关键是掌握好三角函数特别是正弦函数、余弦函数的单调性,最值,周期及图象等性质,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |