题目内容
过椭圆C: 的一个焦点F且垂直于x轴的直线交椭圆于点
的一个焦点F且垂直于x轴的直线交椭圆于点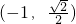 .
.
(1)求椭圆C的方程;
(2)椭圆C的左、右顶点A、B,左、右焦点分别为F1,F2,P为以F1F2为直径的圆上异于F1,F2的动点,问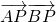 是否为定值,若是求出定值,不是说明理由?
是否为定值,若是求出定值,不是说明理由?
(3)是否存在过点Q(-2,0)的直线l与椭圆C交于两点M、N,使得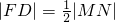 (其中D为弦MN的中点)?若存在,求出直线l的方程:若不存在,请说明理由.
(其中D为弦MN的中点)?若存在,求出直线l的方程:若不存在,请说明理由.
解:(1)由题设知c=1, ①,又a2=b2+c2,即a2=b2+1②,
①,又a2=b2+c2,即a2=b2+1②,
联立①②解得a2=2,b2=1,
所以椭圆C的方程为 ;
;
(2)由(1)知,A(- ,0),B(
,0),B( ,0),F1(-1,0),F2(1,0),
,0),F1(-1,0),F2(1,0),
设P(x0,y0)(x0≠±1),则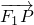 =(x0+1,y0),
=(x0+1,y0),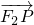 =(x0-1,y0),
=(x0-1,y0),
因为P为以F1F2为直径的圆上的动点,所以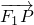 ⊥
⊥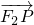 ,即
,即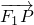 •
•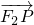 =0,
=0,
所以(x0+1)(x0-1)+y02=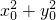 -1=0,即
-1=0,即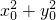 =1,
=1,
所以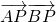 =(
=( ,y0)•(
,y0)•(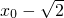 ,y0)═(
,y0)═( )•(
)•(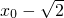 )+y02=
)+y02=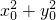 -2=1-2=-1.
-2=1-2=-1.
故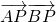 是定值,为-1.
是定值,为-1.
(3)假设存在满足条件的直线l,设直线l的方程为y=k(x+2),
由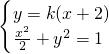 得(2k2+1)x2+8k2x+8k2-2=0,则△=64k4-4(2k2+1)(8k2-2)>0,即
得(2k2+1)x2+8k2x+8k2-2=0,则△=64k4-4(2k2+1)(8k2-2)>0,即 ③,
③,
设M(x1,y1),N(x2,y2),则 ,
,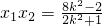 ,
,
由D为弦MN的中点,且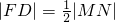 ,得FM⊥FN,即
,得FM⊥FN,即 ,
,
所以(x1+1,y1)•(x2+1,y2)=(x1+1)•(x2+1)+y1y2=x1x2+x1+x2+1+k2(x1+1)(x2+1)=0,即(k2+1)x1x2+(2k2+1)(x1+x2)+4k2+1=0,
所以(k2+1)• +(2k2+1)•
+(2k2+1)• +4k2+1=0,
+4k2+1=0,
解得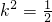 ,不满足③式,
,不满足③式,
故不存在这样的直线l.
分析:(1)由题设知c=1, ,又a2=b2+c2,联立方程组解出即可;
,又a2=b2+c2,联立方程组解出即可;
(2)设P(x0,y0)(x0≠±1),P为以F1F2为直径的圆上的动点,所以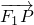 ⊥
⊥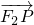 ,即
,即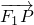 •
•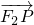 =0,利用向量数量积运算可得
=0,利用向量数量积运算可得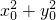 =1,由此可算出
=1,由此可算出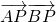 的值;
的值;
(3)假设存在满足条件的直线l,设直线l的方程为y=k(x+2),由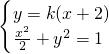 得(2k2+1)x2+8k2x+8k2-2=0,则△>0③,设M(x1,y1),N(x2,y2),由D为弦MN的中点,且
得(2k2+1)x2+8k2x+8k2-2=0,则△>0③,设M(x1,y1),N(x2,y2),由D为弦MN的中点,且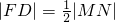 ,得M⊥FN,即
,得M⊥FN,即 ,根据向量数量积运算及韦达定理可表示为k的方程,解出k值,验证是否满足③式即可;
,根据向量数量积运算及韦达定理可表示为k的方程,解出k值,验证是否满足③式即可;
点评:本题考查直线与圆锥曲线的位置关系、平面向量数量积的运算及椭圆方程的求解,考查学生综合运用所学知识分析解决问题的能力,综合性强,能力要求较高.
 ①,又a2=b2+c2,即a2=b2+1②,
①,又a2=b2+c2,即a2=b2+1②,联立①②解得a2=2,b2=1,
所以椭圆C的方程为
 ;
;(2)由(1)知,A(-
 ,0),B(
,0),B( ,0),F1(-1,0),F2(1,0),
,0),F1(-1,0),F2(1,0),设P(x0,y0)(x0≠±1),则
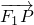 =(x0+1,y0),
=(x0+1,y0),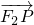 =(x0-1,y0),
=(x0-1,y0),因为P为以F1F2为直径的圆上的动点,所以
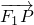 ⊥
⊥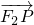 ,即
,即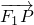 •
•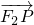 =0,
=0,所以(x0+1)(x0-1)+y02=
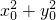 -1=0,即
-1=0,即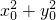 =1,
=1,所以
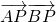 =(
=( ,y0)•(
,y0)•(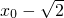 ,y0)═(
,y0)═( )•(
)•(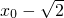 )+y02=
)+y02=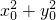 -2=1-2=-1.
-2=1-2=-1.故
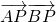 是定值,为-1.
是定值,为-1.(3)假设存在满足条件的直线l,设直线l的方程为y=k(x+2),
由
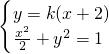 得(2k2+1)x2+8k2x+8k2-2=0,则△=64k4-4(2k2+1)(8k2-2)>0,即
得(2k2+1)x2+8k2x+8k2-2=0,则△=64k4-4(2k2+1)(8k2-2)>0,即 ③,
③,设M(x1,y1),N(x2,y2),则
 ,
,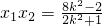 ,
,由D为弦MN的中点,且
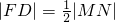 ,得FM⊥FN,即
,得FM⊥FN,即 ,
,所以(x1+1,y1)•(x2+1,y2)=(x1+1)•(x2+1)+y1y2=x1x2+x1+x2+1+k2(x1+1)(x2+1)=0,即(k2+1)x1x2+(2k2+1)(x1+x2)+4k2+1=0,
所以(k2+1)•
 +(2k2+1)•
+(2k2+1)• +4k2+1=0,
+4k2+1=0,解得
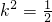 ,不满足③式,
,不满足③式,故不存在这样的直线l.
分析:(1)由题设知c=1,
 ,又a2=b2+c2,联立方程组解出即可;
,又a2=b2+c2,联立方程组解出即可;(2)设P(x0,y0)(x0≠±1),P为以F1F2为直径的圆上的动点,所以
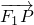 ⊥
⊥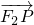 ,即
,即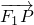 •
•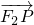 =0,利用向量数量积运算可得
=0,利用向量数量积运算可得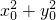 =1,由此可算出
=1,由此可算出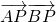 的值;
的值;(3)假设存在满足条件的直线l,设直线l的方程为y=k(x+2),由
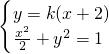 得(2k2+1)x2+8k2x+8k2-2=0,则△>0③,设M(x1,y1),N(x2,y2),由D为弦MN的中点,且
得(2k2+1)x2+8k2x+8k2-2=0,则△>0③,设M(x1,y1),N(x2,y2),由D为弦MN的中点,且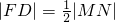 ,得M⊥FN,即
,得M⊥FN,即 ,根据向量数量积运算及韦达定理可表示为k的方程,解出k值,验证是否满足③式即可;
,根据向量数量积运算及韦达定理可表示为k的方程,解出k值,验证是否满足③式即可;点评:本题考查直线与圆锥曲线的位置关系、平面向量数量积的运算及椭圆方程的求解,考查学生综合运用所学知识分析解决问题的能力,综合性强,能力要求较高.

练习册系列答案
相关题目


 的一个焦点为F(1,0),且过点(2,0).
的一个焦点为F(1,0),且过点(2,0).
 如图所示,椭圆C:
如图所示,椭圆C: 。
。 的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形;
的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形; 的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;
的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;