题目内容
方程 所表示的曲线为
所表示的曲线为
 所表示的曲线为
所表示的曲线为 A.焦点在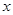 轴上的椭圆 轴上的椭圆 | B.焦点在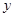 轴上的椭圆 轴上的椭圆 |
C.焦点在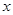 轴上的双曲线 轴上的双曲线 | D.焦点在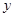 轴上的双曲线 轴上的双曲线 |
D
此题考查圆锥曲线的知识


 所以曲线是焦点在y轴的双曲线
所以曲线是焦点在y轴的双曲线
答案 D


 所以曲线是焦点在y轴的双曲线
所以曲线是焦点在y轴的双曲线答案 D

练习册系列答案
相关题目
题目内容
 所表示的曲线为
所表示的曲线为 A.焦点在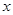 轴上的椭圆 轴上的椭圆 | B.焦点在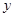 轴上的椭圆 轴上的椭圆 |
C.焦点在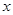 轴上的双曲线 轴上的双曲线 | D.焦点在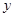 轴上的双曲线 轴上的双曲线 |


 所以曲线是焦点在y轴的双曲线
所以曲线是焦点在y轴的双曲线