Question

【题目】椭圆的左、右焦点分别是，且点在上，抛物线与椭圆交于四点

（I）求的方程；

（Ⅱ）试探究坐标平面上是否存在定点，满足?（若存在，求出的坐标；若不存在，需说明理由.）

Answer 1

【答案】(Ⅰ) ；(Ⅱ)答案见解析.

【解析】试题分析：（I）根据椭圆定义求，再根据c求b，即得的方程；（Ⅱ）根据椭圆和抛物线对称性得转化为研究的垂直平分线和轴的交点是否为定点.联立抛物线方程与椭圆方程，利用韦达定理以及中点公式得，再根据直线斜率公式得AB斜率，表示垂直平分线方程，求得其和轴的交点为，即得结论.

试题解析：（I）依题意有：

所以

所以椭圆的方程为：

（Ⅱ）法一：由于椭圆和抛物线都关于轴对称，故它们的交点也关于轴对称，不妨设，则

若存在点满足条件，则点在轴上，设，

联立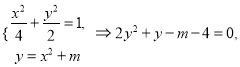

则，

由于

所以

又

所以

则

即

故坐标平面上存在定点，满足

法二：由于椭圆和抛物线都关于轴对称，故它们的交点也关于轴对称，不妨设，则 的中心

依题意，只要探究的垂直平分线和轴的交点是否为定点.

联立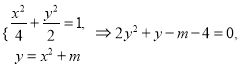

则，

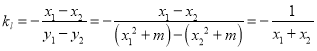
所以，直线：

令得： 为定值，

故坐标平面上存在定点，满足.