题目内容
【题目】已知函数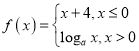 且点
且点![]() 在函数
在函数![]() 的图象上.
的图象上.
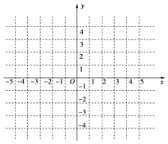
(1)求函数![]() 的解析式,并在图中的直角坐标系中画出函数
的解析式,并在图中的直角坐标系中画出函数![]() 的图象;
的图象;
(2)求不等式![]() 的解集;
的解集;
(3)若方程![]() 有两个不相等的实数根,求实数
有两个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)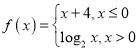 ,图像见解析(2)
,图像见解析(2)![]() (3)
(3)![]()
【解析】
(1)将点![]() 代入
代入![]() 中,即可求解的值,进而求得函数
中,即可求解的值,进而求得函数![]() 的解析式,画出函数f(x)的图象.
的解析式,画出函数f(x)的图象.
(2)分为![]() 两种情况分别求解不等式
两种情况分别求解不等式![]() ,再取并集即可得不等式
,再取并集即可得不等式![]() 的解集.
的解集.
(3)欲求满足方程![]() 有两个不相等的实数根的取值范围,可使函数
有两个不相等的实数根的取值范围,可使函数![]() 与
与![]() 有两个不同的交点,画出二者的图象即可判断出实数
有两个不同的交点,画出二者的图象即可判断出实数![]() 的取值范围.
的取值范围.
解:(1)由![]() 的图象经过点
的图象经过点![]() ,
,
可得![]() ,即
,即![]() ,解得
,解得![]() ,
,
则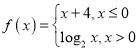 ,
,
函数![]() 的图象如下图:
的图象如下图:
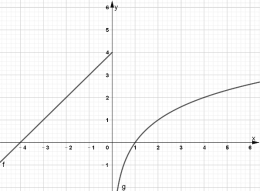
(2)![]() 即为
即为![]() 或
或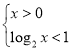 ,
,
即![]() 或
或![]() ,
,
则解集为![]() ;
;
(3)![]() 有两个不相等的实数根,
有两个不相等的实数根,
即有![]() 的图象和直线
的图象和直线![]() 有两个交点,
有两个交点,
由图象可得![]() ,即
,即![]() ,
,
可得![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某工厂生产甲、乙两种产品所得的利润分别为![]() 和
和![]() (万元),事先根据相关资料得出它们与投入资金
(万元),事先根据相关资料得出它们与投入资金![]() (万元)的数据分别如下表和图所示:其中已知甲的利润模型为
(万元)的数据分别如下表和图所示:其中已知甲的利润模型为![]() ,乙的利润模型为
,乙的利润模型为![]() .(
.(![]() 为参数,且
为参数,且![]() ).
).
|
|
|
|
|
|
|
|
|
|
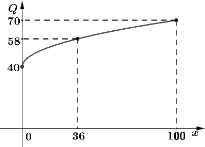
(1)请根据下表与图中数据,分别求出甲、乙两种产品所得的利润与投入资金![]() (万元)的函数模型
(万元)的函数模型
(2)今将![]() 万资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于
万资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于![]() 万元.设对乙种产品投入资金
万元.设对乙种产品投入资金![]() (万元),并设总利润为
(万元),并设总利润为![]() (万元),如何分配投入资金,才能使总利润最大?并求出最大总利润.
(万元),如何分配投入资金,才能使总利润最大?并求出最大总利润.

