题目内容
在椭圆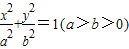
中，F1，F2分别是其左右焦点，若|PF1|=2|PF2|，则该椭圆离心率的取值范围是（ ）A．
B．
C．
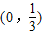
D．
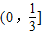
【答案】分析：先根据椭圆的定义求得|PF1|+|PF2|=2a，进而根据|PF1|=2|PF2|求得|PF2|利用椭圆的几何性质可知|PF2|≥a-c，求得a和c的不等式关系，进而求得e的范围，最后根据e＜1，综合可求得椭圆离心率的取值范围．
解答：解：根据椭圆定义|PF1|+|PF2|=2a，将设|PF1|=2|PF2|代入得
，
根据椭圆的几何性质，|PF2|≥a-c，故
，即a≤3c
，故
，即
，又e＜1，
故该椭圆离心率的取值范围是
．
故选B．
点评：本题主要考查了椭圆的定义，考查了学生对基础知识的理解和掌握．
解答：解：根据椭圆定义|PF1|+|PF2|=2a，将设|PF1|=2|PF2|代入得
，根据椭圆的几何性质，|PF2|≥a-c，故
，即a≤3c，故
，即，又e＜1，故该椭圆离心率的取值范围是
．故选B．
点评：本题主要考查了椭圆的定义，考查了学生对基础知识的理解和掌握．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
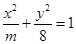中，F1，F2分别为椭圆的左、右焦点，B、D分别
的值；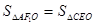
时，求直线AC的方程．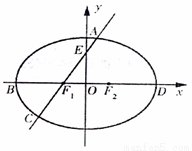
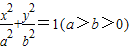中，F1，F2为其左、右焦点，以F1F2为直径的圆与椭圆交于A，B，C，D四个点，若F1，F2，A，B，C，D恰好为一个正六边形的六个顶点，则椭圆的离心率为（ ）
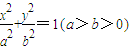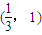
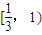
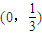
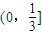
中，F1，F2分别是其左右焦点，若|PF1|=2|PF2|，则该椭圆离心率的取值范围是（ ）
中，F1，F2分别是其左右焦点，若|PF1|=2|PF2|，则该椭圆离心率的取值范围是（ ）
