题目内容
已知函数
.
（1）求
的最小正周期及单调递减区间；
（2）若在区间
上的最大值与最小值的和为
，求
的值.
【答案】
（1）
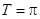；单调递减区间是
（
）．
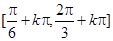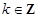（2）
.
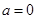【解析】
试题分析：（1）本小题首先需要对函数的解析式进行化简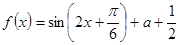
，然后根据周期公式可求得函数的周期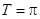，再结合正弦函数的单调区间分析出函数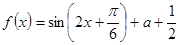的单调递减区间（
）；
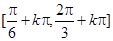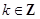（2）本小题首先根据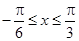
，求得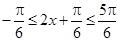
，然后分别求得函数的最大值和最小值，其和为
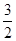可得.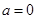
试题解析：（1）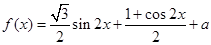
.
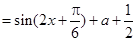所以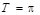
．
由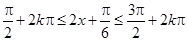
，
得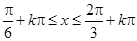
．
故函数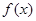
的单调递减区间是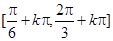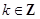（）． 7分
（2）因为，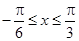
所以．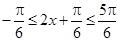
所以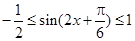
．
因为函数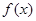在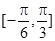
上的最大值与最小值的和
，
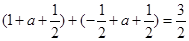所以．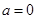
13分
考点：三角函数的图像与性质.
练习册系列答案
相关题目
．
的定义域
；
，求实数
的值．
．
在（0，+∞）上是减函数．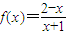
；
成立，若存在求出x；若不存在，请说明理由．
令
的定义域；
的奇偶性，并予以证明；
，猜想
之间的关系并证明.
，
的定义域；（2）证明：
，求
的取值范围。