题目内容
已知平面向量 =(
=( ,
, ),
), =(
=( ,
, ).
).
(1)证明: ⊥
⊥ ;
;
(2)若存在不同时为零的实数k和t,使 =
= +(t2-k)
+(t2-k) ,
, =-s
=-s +t
+t ,且
,且 ⊥
⊥ ,试求s=f(t)的函数关系式;
,试求s=f(t)的函数关系式;
(3)若s=f(t)在[1,+∞)上是增函数,试求k的取值范围.
(本小题满分12分)
解:(1)证明:由题知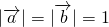 ,且
,且 ,
,
∴ .(4分)
.(4分)
(2)由于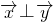 ,则
,则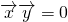 ,
,
从而-s| |2+(t+sk-st2)
|2+(t+sk-st2) +t(t2-k)|
+t(t2-k)| |2=0,
|2=0,
故s=f(t)=t3-kt.(8分)
(3)设t1>t2≥1,
则 -kt2)
-kt2)
=(t1-t2)( ),
),
∵s=f(t)在[1,+∞)上是增函数,
∴ ,
,
即k< 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
∵ >3,
>3,
∴只需k≤3即可.(12分)
分析:(1)由题知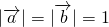 ,且
,且 ,能够证明
,能够证明 .
.
(2)由于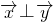 ,则
,则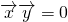 ,从而-s|
,从而-s| |2+(t+sk-st2)
|2+(t+sk-st2) +t(t2-k)|
+t(t2-k)| |2=0,由此能够求出s=f(t)=t3-kt.
|2=0,由此能够求出s=f(t)=t3-kt.
(3)设t1>t2≥1,则 -kt2)=(t1-t2)(
-kt2)=(t1-t2)( ),由s=f(t)在[1,+∞)上是增函数,知k<
),由s=f(t)在[1,+∞)上是增函数,知k< 在[1,+∞)上恒成立,由此能求出k的范围.
在[1,+∞)上恒成立,由此能求出k的范围.
点评:本题考查向量垂直的证明,考查函数解析式的求法,考查实数的取值范围的求法,是基础题.解题时要认真审题,仔细解答.
解:(1)证明:由题知
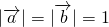 ,且
,且 ,
,∴
 .(4分)
.(4分)(2)由于
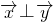 ,则
,则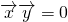 ,
,从而-s|
 |2+(t+sk-st2)
|2+(t+sk-st2) +t(t2-k)|
+t(t2-k)| |2=0,
|2=0,故s=f(t)=t3-kt.(8分)
(3)设t1>t2≥1,
则
 -kt2)
-kt2)=(t1-t2)(
 ),
),∵s=f(t)在[1,+∞)上是增函数,
∴
 ,
,即k<
 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,∵
 >3,
>3,∴只需k≤3即可.(12分)
分析:(1)由题知
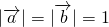 ,且
,且 ,能够证明
,能够证明 .
.(2)由于
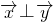 ,则
,则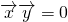 ,从而-s|
,从而-s| |2+(t+sk-st2)
|2+(t+sk-st2) +t(t2-k)|
+t(t2-k)| |2=0,由此能够求出s=f(t)=t3-kt.
|2=0,由此能够求出s=f(t)=t3-kt.(3)设t1>t2≥1,则
 -kt2)=(t1-t2)(
-kt2)=(t1-t2)( ),由s=f(t)在[1,+∞)上是增函数,知k<
),由s=f(t)在[1,+∞)上是增函数,知k< 在[1,+∞)上恒成立,由此能求出k的范围.
在[1,+∞)上恒成立,由此能求出k的范围.点评:本题考查向量垂直的证明,考查函数解析式的求法,考查实数的取值范围的求法,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知平面向量
=(1,-3),
=(4,-2),λ
+
与
垂直,则λ是( )
| a |
| b |
| a |
| b |
| a |
| A、-1 | B、1 | C、-2 | D、2 |
已知平面向量
,
满足|
|=1,|
|=2,
与
的夹角为60°,则“m=1”是“(
-m
)⊥
”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |