Question

17．设函数f（x）=x²-2|x|-1（-3≤x≤5）
（1）讨论函数的奇偶数；
（2）讨论函数的单调性；
（3）x为何值时，f（x）＞0；
（4）求函数的最大值和最小值；
（5）画出函数的图象．

Answer 1

分析 画出函数f（x）=x²-2|x|-1（-3≤x≤5）的图象，结合函数的图象，可分析出函数的奇偶性，单调性，最值，及x为何值时，f（x）＞0；

解答 解：函数f（x）=x²-2|x|-1（-3≤x≤5）的图象如下图所示：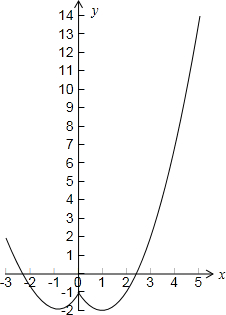

由图可得：
（1）函数的定义域不关于原点对称，
故函数为非奇非偶函数；
（2）函数在区间[-3，-1]和[0，1]上为减函数；
函数在[-1，0]和[1，5]上为增函数；
（3）当x＞0时，解f（x）=x²-2x-1=0得：x=1+$\sqrt{2}$，
当x＜0时，解f（x）=x²+2x-1=0得：x=-1-$\sqrt{2}$，
故当x∈[-3，-1-$\sqrt{2}$]∪[1+$\sqrt{2}$，5]时，f（x）＞0；
（4）当x=5时，函数的最大值为14，
当x=±1时，函数的最小值为-2；
（5）画出函数的图象如上图所示．

点评 本题考查的知识点是二次函数的图象和性质，分段函数的应用，画出函数图象，数形结合是解答的关键．