题目内容
设tanα=3,求下列各式的值.(1)![]() ;
;
(2)sinαcosα;
(3)3sin2α+2.
思路分析:若由tanα=3,求sinα,cosα的值,则要将α分一、三象限讨论,那么sinα,cosα的正负号就不确定了,所以解本题要注意应用基本关系式.对于(2)、(3)两题还应注意“1”的代换.
解:(1)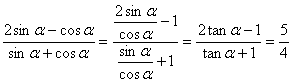 .
.
(2)∵![]() ,
,
又将tanα=3代入,得![]() .
.
(3)3sin2α+2=3sin2α+2(sin2α+cos2α)
=5sin2α+2cos2α=![]()
=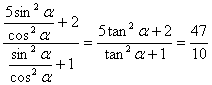 .
.
方法归纳 这类题的解法体现了化归思想的应用,即对只含有正弦、余弦的齐次式,可根据同角三角函数的商数关系,通过除以某一齐次项,转化成只含有正切的式子.这种化弦为切的技巧,有着广泛的应用.
深化升华 凡是分子、分母是某个角的正弦、余弦函数的齐次多项式,都可以用这个角的正切函数来表示.在三角知识中“1”的变换很多,除了平方关系之外,还有为了凑出某个公式的条件,也可以乘以“1”.

练习册系列答案
相关题目
 ,设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值.
,设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值.
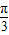 )(x∈R),且
)(x∈R),且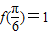 .
.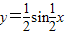 的图象;
的图象;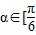 ,
,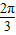 ,
,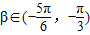 ,
,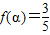 ,f(β)=-
,f(β)=- ,
,