题目内容
已知椭圆M: (a>b>0)的离心率为
(a>b>0)的离心率为 ,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.
(Ⅰ)求椭圆M的方程;
(Ⅱ)设直线l:x=ky+m与椭圆M交手A,B两点,若以AB为直径的圆经过椭圆的右顶点C,求m的值.
解:(Ⅰ)由题意,可得  ,即
,即 ,…(1分)
,…(1分)
又椭圆的离心率为 ,即
,即 ,…(2分)
,…(2分)
所以a=3,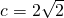 ,
,
所以b2=a2-c2=1,…(3分)
所以椭圆M的方程为 .…(4分)
.…(4分)
(Ⅱ)由 消去x得(k2+9)y2+2kmy+m2-9=0.…(5分)
消去x得(k2+9)y2+2kmy+m2-9=0.…(5分)
设A(x1,y1),B(x2,y2),有 ,
, .①…(6分)
.①…(6分)
因为以AB为直径的圆过椭圆右顶点C(3,0),所以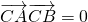 .…(7分)
.…(7分)
由 ,
, ,得 (x1-3)(x2-3)+y1y2=0.…(8分)
,得 (x1-3)(x2-3)+y1y2=0.…(8分)
将x1=ky1+m,x2=ky2+m代入上式,
得 ,…(10分)
,…(10分)
将 ①代入上式得
解得 ,或m=3.…(12分)
,或m=3.…(12分)
分析:(Ⅰ)根据椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 ,椭圆的离心率,建立方程,利用b2=a2-c2,可求椭圆M的方程;
,椭圆的离心率,建立方程,利用b2=a2-c2,可求椭圆M的方程;
(Ⅱ)由直线与椭圆方程联立,消元,由以AB为直径的圆过椭圆右顶点C(3,0),可得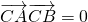 ,结合数量积公式及韦达定理,即可求m的值.
,结合数量积公式及韦达定理,即可求m的值.
点评:本题考查椭圆的标准方程与几何性质,考查直线与椭圆的位置关系,考查向量知识的运用,考查韦达定理,联立方程,利用韦达定理是解题的关键.
 ,即
,即 ,…(1分)
,…(1分)又椭圆的离心率为
 ,即
,即 ,…(2分)
,…(2分)所以a=3,
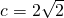 ,
,所以b2=a2-c2=1,…(3分)
所以椭圆M的方程为
 .…(4分)
.…(4分)(Ⅱ)由
 消去x得(k2+9)y2+2kmy+m2-9=0.…(5分)
消去x得(k2+9)y2+2kmy+m2-9=0.…(5分)设A(x1,y1),B(x2,y2),有
 ,
, .①…(6分)
.①…(6分)因为以AB为直径的圆过椭圆右顶点C(3,0),所以
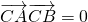 .…(7分)
.…(7分)由
 ,
, ,得 (x1-3)(x2-3)+y1y2=0.…(8分)
,得 (x1-3)(x2-3)+y1y2=0.…(8分)将x1=ky1+m,x2=ky2+m代入上式,
得
 ,…(10分)
,…(10分)将 ①代入上式得

解得
 ,或m=3.…(12分)
,或m=3.…(12分)分析:(Ⅰ)根据椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
 ,椭圆的离心率,建立方程,利用b2=a2-c2,可求椭圆M的方程;
,椭圆的离心率,建立方程,利用b2=a2-c2,可求椭圆M的方程;(Ⅱ)由直线与椭圆方程联立,消元,由以AB为直径的圆过椭圆右顶点C(3,0),可得
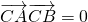 ,结合数量积公式及韦达定理,即可求m的值.
,结合数量积公式及韦达定理,即可求m的值.点评:本题考查椭圆的标准方程与几何性质,考查直线与椭圆的位置关系,考查向量知识的运用,考查韦达定理,联立方程,利用韦达定理是解题的关键.

练习册系列答案
相关题目
 (a>b>0)的离心率为
(a>b>0)的离心率为 ,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.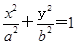 (a>b>0)的离心率为
(a>b>0)的离心率为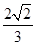 ,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.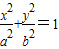 (a>b>0)的离心率为
(a>b>0)的离心率为 ,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
. (a>b>0)的离心率为
(a>b>0)的离心率为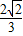 ,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
. (a>b>0)的离心率为
(a>b>0)的离心率为 ,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.